Question

【题目】（1）问题发现：如图1，是等边三角形，点是边上的一点，过点作交于，则线段与有何数量关系是______；

（2）拓展探究：如图2，将绕点逆时针旋转角，上面的结论是否仍然成立？如果成立，请就图2给出的情况加以证明；

（3）问题解决：如果的边长为4，，直接写出当旋转、、在同一条直线上时的长.

Answer 1

【答案】（1），见解析；（2）仍然成立，见解析；（3）或.

【解析】

（1）根据等边三角形的性质得到∠B=∠C=60°，AB=AC，再利用平行的性质证得∠ADE=∠AED，从而得到AD=AE，最后根据线段之间的关系即可得到结论；

（2）证明△BAD≌△CAE，即可得到结论；

（3）分顺时针旋转和逆时针旋转两种情况，画出图形，然后根据线段之间的关系即可计算出BE的长度.

解：（1）BD=CE，理由是：

∵△ABC是等边三角形，

∴AB=AC，∠B=∠C=60°，

∵DE∥BC，

∴∠ADE=∠B，∠AED=∠C，

∴∠ADE=∠AED=60°，

∴AD=AE，

∴AB－AD=AC－AE，

∴BD=CE；

（2）仍然成立.

证明：∵是等边三角形，DE∥BC，

∴是等边三角形，

∴，，，

∴，即，

∴，

∴；

（3）当顺时针旋转到、、在同一条直线上时：

∴BE=AB－AE=4－2=2，

当逆时针旋转到、、在同一条直线上时：

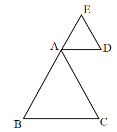
∴BE=AB+AE=4+2=6，

综上所述，BE=2或6.