
分析 (1)利用待定系数法即可解决问题.
(2)根据题意列出方程求出即可.
(3)构建二次函数,利用二次函数的性质即可解决问题.
解答 解:(1)设y=kx+b,
把(22,36)与(24,32)代入得:$\left\{\begin{array}{l}{22k+b=36}\\{24k+b=32}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=80}\end{array}\right.$,
则y=-2x+80;
(2)设当饰品店每周销售这种饰品获得150元的利润时,每件饰品的销售单价是x元,
根据题意得:(x-20)y=150,则(x-20)(-2x+80)=150,
整理得:x2-60x+875=0,(x-25)(x-35)=0,
解得:x1=25,x2=35(不合题意舍去),
答:每件饰品的销售单价是25元;
(3)由题意可得:w=(x-20)(-2x+80)
=-2x2+120x-1600=-2(x-30)2+200,…(8分)
此时当x=30时,w最大,但又∵x<30时,y随x的增大而增大,
∴当售价不低于22元且不高于28元时,
有x=28,w最大=-2(28-30)2+200=192(元),…(9分)
答:该饰品销售单价定为28元时,才能使饰品店销售这种饰品所获利润最大,最大利润是192元.
点评 本题考查二次函数的应用、一元二次方程的应用、待定系数法等知识,解题的关键是灵活应用这些知识解决问题,学会构建二次函数解决最值问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
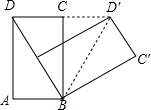 如图,把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),求∠CBC′的度数.
如图,把矩形ABCD以B为中心,按照顺时针方向旋转到A′BC′D′的位置(点A′落在对角线BD上,点D′在DC的延长线上),求∠CBC′的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O与△ABC各边分别切于点D,E,F,
如图,⊙O与△ABC各边分别切于点D,E,F,查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{x}{2}$ | B. | y=2x | C. | y=-$\frac{x}{3}$ | D. | y=-2+5x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com