
ĄūĖâÄŋĄŋČįÍžĢŽÖąÏßyĢ―Đ![]() x+4ÓëŨøąęÖá·Öąð―ŧÓÚĩãAĄĒBĢŽÓëÖąÏßyĢ―x―ŧÓÚĩãCĢŪÔÚÏßķÎOAÉÏĢŽķŊĩãQŌÔÃŋÃë1ļöĩĨÎŧģĪķČĩÄËŲķČīÓĩãOģö·ĒÏōĩãAŨöÔČËŲÔËķŊĢŽÍŽĘąķŊĩãPīÓĩãAģö·ĒÏōĩãOŨöÔČËŲÔËķŊĢŽĩąĩãPĄĒQÆäÖÐŌŧĩãÍĢÖđÔËķŊĘąĢŽÁíŌŧĩãŌēÍĢÖđÔËķŊĢŪ·ÖąðđýĩãPĄĒQŨũxÖáĩÄīđÏßĢŽ―ŧÖąÏßABĄĒOCÓÚĩãEĄĒFĢŽÁŽ―ÓEFĢŪČôÔËķŊĘąžäΊtÃëĢŽÔÚÔËķŊđýģĖÖÐËÄąßÐÎPEFQŨÜΊūØÐÎĢĻĩãPĄĒQÖØšÏģýÍâĢĐĢŪ
x+4ÓëŨøąęÖá·Öąð―ŧÓÚĩãAĄĒBĢŽÓëÖąÏßyĢ―x―ŧÓÚĩãCĢŪÔÚÏßķÎOAÉÏĢŽķŊĩãQŌÔÃŋÃë1ļöĩĨÎŧģĪķČĩÄËŲķČīÓĩãOģö·ĒÏōĩãAŨöÔČËŲÔËķŊĢŽÍŽĘąķŊĩãPīÓĩãAģö·ĒÏōĩãOŨöÔČËŲÔËķŊĢŽĩąĩãPĄĒQÆäÖÐŌŧĩãÍĢÖđÔËķŊĘąĢŽÁíŌŧĩãŌēÍĢÖđÔËķŊĢŪ·ÖąðđýĩãPĄĒQŨũxÖáĩÄīđÏßĢŽ―ŧÖąÏßABĄĒOCÓÚĩãEĄĒFĢŽÁŽ―ÓEFĢŪČôÔËķŊĘąžäΊtÃëĢŽÔÚÔËķŊđýģĖÖÐËÄąßÐÎPEFQŨÜΊūØÐÎĢĻĩãPĄĒQÖØšÏģýÍâĢĐĢŪ
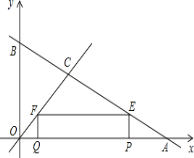
ĢĻ1ĢĐĮóĩãPÔËķŊĩÄËŲķČĘĮķāÉŲĢŋ
ĢĻ2ĢĐĩątΊķāÉŲÃëĘąĢŽūØÐÎPEFQΊÕý·―ÐÎĢŋ
Ąūīð°ļĄŋĢĻ1ĢĐĩãPÔËķŊĩÄËŲķČĘĮÃŋÃë2ļöĩĨÎŧģĪķČĢŧĢĻ2ĢĐtĢ―2ŧō4Ģŧ
Ąū―âÎöĄŋ
ĢĻ1ĢĐÏČĮóĩÃAĢŽBÁ―ĩãŨøąęĢŽĩÃĩ―![]() ĩÄÖĩĢŽÔŲļųūÝÏāËÆČý―ĮÐÎķÔÓĶąßģÉąČĀýĩÃĩ―APÓëEPĩÄąČÖĩĢŽ―øķøĩÃĩ―ĩãPĩÄËŲķČĢŧ
ĩÄÖĩĢŽÔŲļųūÝÏāËÆČý―ĮÐÎķÔÓĶąßģÉąČĀýĩÃĩ―APÓëEPĩÄąČÖĩĢŽ―øķøĩÃĩ―ĩãPĩÄËŲķČĢŧ
ĢĻ2ĢĐ·ÖQĢŽPÁ―ĩãÏāÓöĮ°šóÁ―ÖÖĮéŋö―øÐÐĖÖÂÛĢŽĩąPQĢ―PEĘąĢŽūØÐÎPEFQΊÕý·―ÐÎĢŽÓÉÓÃđØÓÚtĩÄĘ―ŨÓąíĘūļũÏßķÎĩÄģĪĢŽČŧšóĮóģötĩÄÖĩžīŋÉ.
―âĢšĢĻ1ĢĐĄßÖąÏßyĢ―Đ![]() x+4ÓëŨøąęÖá·Öąð―ŧÓÚĩãAĄĒBĢŽ
x+4ÓëŨøąęÖá·Öąð―ŧÓÚĩãAĄĒBĢŽ
ĄāxĢ―0ĘąĢŽyĢ―4ĢŽyĢ―0ĘąĢŽxĢ―8ĢŽ
Ąā![]() ĢŽ
ĢŽ
ĩątÃëĘąĢŽQOĢ―FQĢ―tĢŽÔōEPĢ―tĢŽ
ĄßEPĄÎBOĢŽ
Ąā![]() ĢŽ
ĢŽ
ĄāAPĢ―2tĢŽ
ĄßķŊĩãQŌÔÃŋÃë1ļöĩĨÎŧģĪķČĩÄËŲķČīÓĩãOģö·ĒÏōĩãAŨöÔČËŲÔËķŊĢŽ
ĄāĩãPÔËķŊĩÄËŲķČĘĮÃŋÃë2ļöĩĨÎŧģĪķČĢŧ
ĢĻ2ĢĐČįÍžĢŽĩąPQĢ―PEĘąĢŽūØÐÎPEFQΊÕý·―ÐÎĢŽ
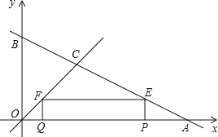
ÔōĄßOQĢ―FQĢ―tĢŽPAĢ―2tĢŽ
ĄāQPĢ―8ĐtĐ2tĢ―8Đ3tĢŽ
Ąā8Đ3tĢ―tĢŽ
―âĩÃĢštĢ―2Ģŧ
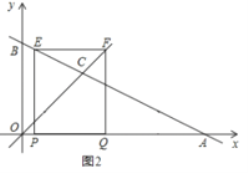
ČįÍž2ĢŽĩąPQĢ―PEĘąĢŽūØÐÎPEFQΊÕý·―ÐÎĢŽ
ĄßOQĢ―tĢŽPAĢ―2tĢŽ
ĄāOPĢ―8Đ2tĢŽ
ĄāQPĢ―tĐĢĻ8Đ2tĢĐĢ―3tĐ8ĢŽ
ĄātĢ―3tĐ8ĢŽ
―âĩÃĢštĢ―4Ģŧ


 ĖėĖėÏōÉÏŌŧąūšÃūíÏĩÁÐīð°ļ
ĖėĖėÏōÉÏŌŧąūšÃūíÏĩÁÐīð°ļ ÐĄŅ§Éú10·ÖÖÓÓĶÓÃĖâÏĩÁÐīð°ļ
ÐĄŅ§Éú10·ÖÖÓÓĶÓÃĖâÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÖąÏß![]() šÍ
šÍ![]() Ïā―ŧÓÚĩã
Ïā―ŧÓÚĩã![]() ĢŽ
ĢŽ![]() ĢŽÔÚÉäÏß
ĢŽÔÚÉäÏß![]() ÉÏČĄŌŧĩã
ÉÏČĄŌŧĩã![]() ĢŽĘđ
ĢŽĘđ![]() ĢŽđýĩã
ĢŽđýĩã![]() Ũũ
Ũũ![]() ÓÚĩã
ÓÚĩã![]() ĢŽ
ĢŽ![]() ĘĮÏßķÎ
ĘĮÏßķÎ![]() ÉÏĩÄŌŧļöķŊĩã(ēŧÓëĩã
ÉÏĩÄŌŧļöķŊĩã(ēŧÓëĩã![]() ÖØšÏ)ĢŽđýĩã
ÖØšÏ)ĢŽđýĩã![]() Ũũ
Ũũ![]() ĩÄīđÏß―ŧÉäÏß
ĩÄīđÏß―ŧÉäÏß![]() ÓÚĩã
ÓÚĩã![]() .
.
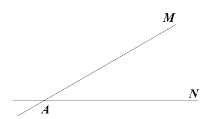
(1)Č·ķĻĩã![]() ĩÄÎŧÖÃĢŽÔÚÏßķÎ
ĩÄÎŧÖÃĢŽÔÚÏßķÎ![]() ÉÏČÎČĄŌŧĩã
ÉÏČÎČĄŌŧĩã![]() ĢŽļųūÝĖâŌâĢŽēđČŦÍžÐÎĢŧ
ĢŽļųūÝĖâŌâĢŽēđČŦÍžÐÎĢŧ
(2)Éč![]() cmĢŽ
cmĢŽ![]() cmĢŽĖ―ūŋšŊĘý
cmĢŽĖ―ūŋšŊĘý![]() ËæŨÔąäÁŋ
ËæŨÔąäÁŋ![]() ĩÄąäŧŊķøąäŧŊĩÄđæÂÉ.
ĩÄąäŧŊķøąäŧŊĩÄđæÂÉ.
ĒŲÍĻđýČĄĩãĄĒŧÍžĄĒēâÁŋĢŽĩÃĩ―ÁË![]() Óë
Óë![]() ĩÄžļŨéķÔÓĶÖĩĢŽČįÏÂąíĢš
ĩÄžļŨéķÔÓĶÖĩĢŽČįÏÂąíĢš
|
|
|
|
|
|
|
|
|
|
|
|
|
(ŌŠĮóĢšēđČŦąíļņĢŽÏāđØĘýÖĩąĢÁôŌŧÎŧÐĄĘý)
ĒÚ)―ĻÁĒÆ―ÃæÖą―ĮŨøąęÏĩ![]() ĢŽÃčģöŌÔēđČŦšóĩÄąíÖÐļũķÔÓĶÖĩΊŨøąęĩÄĩãĢŽŧģöļÚŊĘýĩÄÍžÏóĢŧ
ĢŽÃčģöŌÔēđČŦšóĩÄąíÖÐļũķÔÓĶÖĩΊŨøąęĩÄĩãĢŽŧģöļÚŊĘýĩÄÍžÏóĢŧ

ĒÛ―ášÏŧģöĩÄšŊĘýÍžÏóĢŽ―âūöÎĘĖâĢšĩą![]() Ί
Ί![]() Ðąąß
Ðąąß![]() ÉÏĩÄÖÐÏßĘąĢŽ
ÉÏĩÄÖÐÏßĘąĢŽ![]() ĩÄģĪķČԞΊ_____cm(―áđûąĢÁôŌŧÎŧÐĄĘý).
ĩÄģĪķČԞΊ_____cm(―áđûąĢÁôŌŧÎŧÐĄĘý).
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
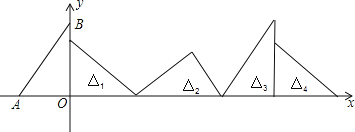
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÖą―ĮŨøąęÏĩÖÐĢŽŌŅÖŠĩãAĢĻĐ3ĢŽ0ĢĐĢŽBĢĻ0ĢŽ4ĢĐĢŽķÔĄũOABÁŽÐøŨũÐýŨŠąäŧŧĢŽŌĀīÎĩÃĩ―Ąũ1ĄĒĄũ2ĄĒĄũ3ĄĒĄũ4ĄĢŽÔōĄũ2020ĩÄÖą―ĮķĨĩãĩÄŨøąęΊ_____ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĄũABCÖÐĢŽĄÏACBĢ―90ĄãĢŽsinAĢ―![]() ĢŽBCĢ―8ĢŽĩãDĘĮABĩÄÖÐĩãĢŽđýĩãBŨũCDĩÄīđÏßĢŽīđŨãΊĩãE.
ĢŽBCĢ―8ĢŽĩãDĘĮABĩÄÖÐĩãĢŽđýĩãBŨũCDĩÄīđÏßĢŽīđŨãΊĩãE.
(1)ĮóÏßķÎCDĩÄģĪĢŧ
(2)ĮócosĄÏABEĩÄÖĩĄĢ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
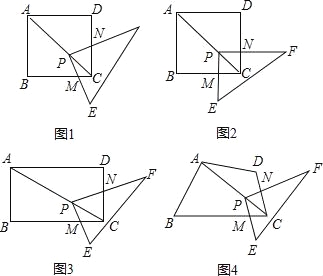
ĄūĖâÄŋĄŋČįÍž1ĢŽĩãPÔÚÕý·―ÐÎABCDĩÄķÔ―ĮÏßACÉÏĢŽÕý·―ÐÎĩÄąßģĪĘĮaĢŽRtĄũPEFĩÄÁ―ĖõÖą―ĮąßPEĄĒPF·Öąð―ŧBCĄĒDCÓÚĩãMĄĒNĢŪ
ĢĻ1ĢĐēŲŨũ·ĒÏÖĢšČįÍž2ĢŽđĖķĻĩãPĢŽĘđĄũPEFČÆĩãPÐýŨŠĢŽĩąPMĄÍBCĘąĢŽËÄąßÐÎPMCNĘĮÕý·―ÐÎĢŪĖîŋÕĢšĒŲĩąAP=2PCĘąĢŽËÄąßÐÎPMCNĩÄąßģĪĘĮ_________ĢŧĒÚĩąAP=nPCĘąĢĻnĘĮÕýĘĩĘýĢĐĢŽËÄąßÐÎPMCNĩÄÃæŧýĘĮ__________ĢŪ
ĢĻ2ĢĐēÂÏëÂÛÖĪ
ČįÍž3ĢŽļÄąäËÄąßÐÎABCDĩÄÐÎŨīΊūØÐÎĢŽAB=aĢŽBC=bĢŽĩãPÔÚūØÐÎABCDĩÄķÔ―ĮÏßACÉÏĢŽRtĄũPEFĩÄÁ―ĖõÖą―ĮąßPEĄĒPF·Öąð―ŧBCĄĒDCÓÚĩãMĄĒNĢŽđĖķĻĩãPĢŽĘđĄũPEFČÆĩãPÐýŨŠĢŽÔō![]() =_______ĢŪ
=_______ĢŪ
ĢĻ3ĢĐÍØÕđĖ―ūŋ
ČįÍž4ĢŽĩąËÄąßÐÎABCDÂúŨãĖõžþĢšĄÏB+ĄÏD=180ĄãĢŽĄÏEPF=ĄÏBADĘąĢŽĩãPÔÚACÉÏĢŽPEĄĒPF·Öąð―ŧBCĢŽCDÓÚMĄĒNĩãĢŽđĖķĻPĩãĢŽĘđĄũPEFČÆĩãPÐýŨŠĢŽĮëĖ―ūŋ![]() ĩÄÖĩĢŽēĒËĩÃũĀíÓÉĢŪ
ĩÄÖĩĢŽēĒËĩÃũĀíÓÉĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽŌŅÖŠĄÏMON=30ĄãĢŽBΊOMÉÏŌŧĩãĢŽBAĄÍONÓÚAĢŽËÄąßÐÎABCDΊÕý·―ÐÎĢŽPΊÉäÏßBMÉÏŌŧķŊĩãĢŽÁŽ―áCPĢŽ―ŦCPČÆĩãCËģĘąÕë·―ÏōÐýŨŠ90ĄãĩÃCEĢŽÁŽ―áBEĢŽČôAB=4ĢŽÔōBEĩÄŨîÐĄÖĩΊ_____ĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
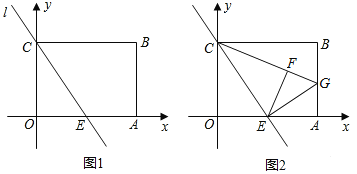
ĄūĖâÄŋĄŋŌŅÖŠūØÐÎOABCĩÄąßģĪOA=4ĢŽAB=3ĢŽEĘĮOAĩÄÖÐĩãĢŽ·ÖąðŌÔOAĄĒOCËųÔÚĩÄÖąÏßΊxÖáĄĒyÖáĢŽ―ĻÁĒČįÍž1ËųĘūĩÄÆ―ÃæÖą―ĮŨøąęÏĩĢŽÖąÏßlūđýCĄĒEÁ―ĩãĢŪ
ĢĻ1ĢĐĮóÖąÏßlĩÄšŊĘýąíīïĘ―Ģŧ
ĢĻ2ĢĐČįÍž2ĢŽÔÚģĪ·―ÐÎOABCÖÐĢŽđýĩãEŨũEGĄÍEC―ŧABÓÚĩãGĢŽÁŽ―ÓCGĢŽ―ŦĄũCOEŅØÖąÏßlÕÛĩþšóĩÃĩ―ĄũCEFĢŽĩãFĮĄšÃÂäÔÚCGÉÏĢŪÖĪÃũĢšGF=GAĢŪ
ĢĻ3ĢĐÔÚĢĻ2ĢĐĩÄĖõžþÏÂĮóËÄąßÐÎAGFEĩÄÃæŧýĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚĄũABCÖÐĢŽADĄĒBEĘĮÖÐÏßĢŽËüÃĮÏā―ŧÓÚĩãFĢŽEGĄÎBCĢŽ―ŧADÓÚĩãGĢŪ
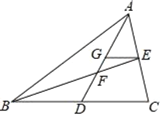
ĢĻ1ĢĐĮóÖĪĢšĄũFGEĄŨĄũFDBĢŧ
ĢĻ2ĢĐĮó![]() ĩÄÖĩĢŪ
ĩÄÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽŌŧļöđ°ÐÎĮÅžÜŋÉŌÔ―üËÆŋīŨũĘĮÓÉĩČŅüĖÝÐÎABD8D1šÍÆäÉÏ·―ĩÄÅŨÎïÏßD1OD8ŨéģÉ.Čô―ĻÁĒČįÍžËųĘūĩÄÖą―ĮŨøąęÏĩĢŽŋįķČAB=44ÃŨĢŽĄÏA=45ĄãĢŽAC1=4ÃŨĢŽĩãD2ĩÄŨøąęΊ(-13ĢŽ-1.69)ĢŽÔōĮÅžÜĩÄđ°ļßOH=________ÃŨ.

ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com