
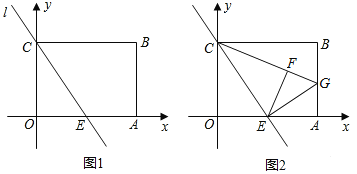
【题目】已知矩形OABC的边长OA=4,AB=3,E是OA的中点,分别以OA、OC所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过C、E两点.
(1)求直线l的函数表达式;
(2)如图2,在长方形OABC中,过点E作EG⊥EC交AB于点G,连接CG,将△COE沿直线l折叠后得到△CEF,点F恰好落在CG上.证明:GF=GA.
(3)在(2)的条件下求四边形AGFE的面积.
【答案】(1)y=![]() x+3;(2)见解析,(3)AGFE的面积是
x+3;(2)见解析,(3)AGFE的面积是![]() .
.
【解析】
(1)根据矩形的性质及中点的定义得出OC=AB=3,OE=2,进而得出E,C两点的坐标,再用待定系数法即可求得直线l的函数表达式;
(2)根据矩形的四个角都是直角得∠COA=∠OAB=90°;根据折叠的性质得到∠COE=∠CFE=90°,OE=EF,进而得到∠EFG=∠EAG=90°;根据中点的定义得OE=AE,根据等量代换得出EF=EA,然后利用HL判断出Rt△EFG≌Rt△EAG,根据全等三角形对应边相等得出GF=GA;
(3)根据折叠的性质知OC=CF=3.根据线段的和差得出BG=AB-AG=3-AG,CG=CF+GF=3+GA,AE=2,在Rt△CBG中,由勾股定理得出关于AG的方程,求解得出AG的长,根据全等三角形的面积相等得出SRt△EFG=SRt△EAG,然后根据S四边形AGFE=2SRt△EAG即可得出答案.
解:(1)∵矩形OABC的边长OA=4,AB=3,E是OA的中点,
∴OC=AB=3,OE=2,
∴E(2,0),C(0,3).
设直线l的解析式y=kx+b(k≠0).
将E(2,0),C(0,3),分别代入y=kx+b得
![]() ,解得
,解得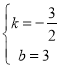 ,
,
∴直线l的解析式y=![]() x+3;
x+3;
(2)∵四边形OABC是矩形,
∴∠COA=∠OAB=90°.
又根据折叠是性质得到∠COE=∠CFE=90°,OE=EF,
∴∠EFG=∠EAG=90°.
又∵E是OA的中点,
∴OE=AE,
∴EF=EA,
∴在Rt△EFG和Rt△EAG中,
![]() ,
,
∴Rt△EFG≌Rt△EAG(HL),
∴GF=GA;
(3)由(2)知,GF=GA,根据折叠的性质知OC=CF=3.
∵BG=AB–AG=3–AG,CG=CF+GF=3+GA,AE=2,
∴在Rt△CBG中,由勾股定理得:
CG2=BC2+BG2,即(3+AG)2=(3–AG)2+42,解得AG=![]() .
.
∵由(2)知,Rt△EFG≌Rt△EAG,
∴SRt△EFG=SRt△EAG,
∴S四边形AGFE=2SRt△EAG=2×![]() AE·AG=2×
AE·AG=2×![]() ×2×
×2×![]() =
=![]() ,即四边形AGFE的面积是
,即四边形AGFE的面积是![]() .
.


科目:初中数学 来源: 题型:
【题目】为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据场调查,在草莓上市销售的30天中,其销售价格![]() (元/公斤)与第
(元/公斤)与第![]() 天之间满足
天之间满足![]() (
(![]() 为正整数),销售量
为正整数),销售量![]() (公斤)与第
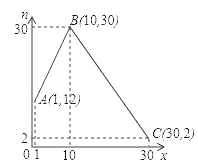
(公斤)与第![]() 天之间的函数关系如图所示:
天之间的函数关系如图所示:
如果李大爷的草莓在上市销售期间每天的维护费用为80元.
(1)求销售量![]() 与第
与第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)求在草莓上市销售的30天中,每天的销售利润![]() 与第
与第![]() 天之间的函数关系式;(日销售利润=日销售额﹣日维护费)
天之间的函数关系式;(日销售利润=日销售额﹣日维护费)
(3)求日销售利润![]() 的最大值及相应的
的最大值及相应的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
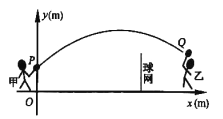
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在![]() 点上正方
点上正方![]() 的
的![]() 处发出一球,羽毛球飞行的高度
处发出一球,羽毛球飞行的高度![]() 与水平距离
与水平距离![]() 之间满足函数表达式
之间满足函数表达式![]() .已知点
.已知点![]() 与球网的水平距离为
与球网的水平距离为![]() ,球网的高度为
,球网的高度为![]() .
.
(1)当![]() 时,①求
时,①求![]() 的值.②通过计算判断此球能否过网.
的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到点![]() 的水平距离为
的水平距离为![]() ,离地面的高度为
,离地面的高度为![]() 的
的![]() 处时,乙扣球成功,求
处时,乙扣球成功,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
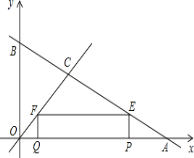
【题目】如图,直线y=﹣![]() x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
(1)求点P运动的速度是多少?
(2)当t为多少秒时,矩形PEFQ为正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.

(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径作⊙O,交于BC的中点D,过点D作直线EF与⊙O相切,交AC于点E,交AB的延长线于点F.若△ABC的面积为△CDE的面积的8倍,则下列结论中,错误的是( )
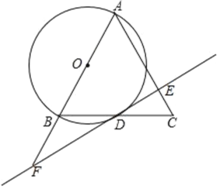
A.AC=2AOB.EF=2AEC.AB=2BFD.DF=2DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是( )
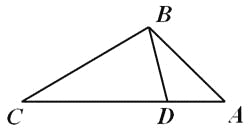
A.∠ABD=∠CB.∠ADB=∠ABCC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
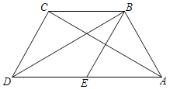
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com