
【题目】如图,以△ABC的一边AB为直径作⊙O,交于BC的中点D,过点D作直线EF与⊙O相切,交AC于点E,交AB的延长线于点F.若△ABC的面积为△CDE的面积的8倍,则下列结论中,错误的是( )
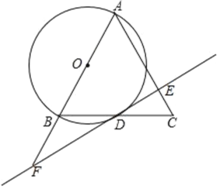
A.AC=2AOB.EF=2AEC.AB=2BFD.DF=2DE
【答案】B
【解析】
连接OD、AD,根据三角形中位线定理判断A选项;根据切线的性质、三角形的面积公式判断B;根据平行线分线段成比例定理判断C、D,即可得到答案.
解:连接OD、AD,
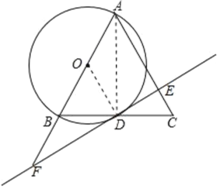
∵OB=OA,BD=DC,
∴AC=2OD,
∵OA=OD,
∴AC=2OD,A正确,不符合题意;
∵EF是⊙O的切线,
∴OD⊥EF,
∵OB=OA,BD=DC,
∴OD∥AC,
∴AE⊥EF,
∵△ABC的面积为△CDE的面积的8倍,D是BC的中点,
∴△ADC的面积为△CDE的面积的4倍,
∴△ADE的面积为△CDE的面积的3倍,
∴AE=3EC,
∴![]() ,
,
∵OD∥AC,
∴![]() ,
,
∴FA=2AE,B错误,符合题意;
AB=2BF,C正确,不符合题意;
∵![]() ,
,
∴DF=2DE,D正确,不符合题意;
故选:B.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大数学家欧拉非常推崇观察能力,他说过,今天已知的许多数的性质,大部分是通过观察发现的,历史上许多大家,都是天才的观察家,化归就是将面临的新问题转化为已经熟悉的规范问题的数学方法,这是一种具有普遍适用性的数学思想方法.如多项式除以多项式可以类比于多位数的除法进行计算:
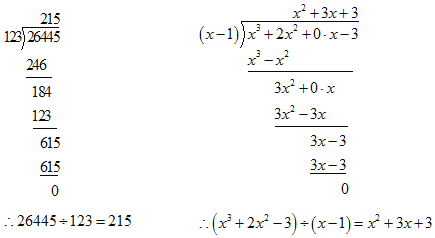
请用以上方法解决下列问题:
(1)计算:(x3+2x2﹣3x﹣10)÷(x﹣2);
(2)若关于x的多项式2x4+5x3+ax2+b能被二项式x+2整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生身体素质,某校决定开展足球、篮球、排球、兵乓球等四项课外体育活动,要求全员参与,并且每名学生只能选择其中一项.为了解选择各种体育活动项目的学生人数,该校随机抽取了部分学生进行调查,并绘制出如下两幅不完整的统计图,请根据统计图回答下列问题:
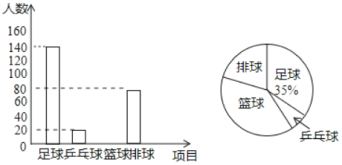
(1)直接写出这次抽样调查的学生人数;
(2)补全条形统计图;
(3)若该学校总人数是1500人,请估计选择篮球项目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+2x+3与一次函数y=3x+5.
(1)两个函数图象相交吗?若相交,有几个交点?
(2)将直线y=3x+5向下平移k个单位,使直线与抛物线只有一个交点,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

请根据以上图表信息解答下列问题:
(1)频数分布表中的![]() ,
,![]() ;
;
(2)在扇形统计图中,“排球”所在的扇形的圆心角为 度;
(3)全校有多少名学生选择参加乒乓球运动?
查看答案和解析>>
科目:初中数学 来源: 题型:
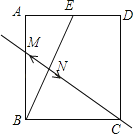
【题目】如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,连接BE,分别以B、E为圆心,以大于![]() 的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
的长为半径作弧,两弧交于点M、N,若直线MN恰好过点C,则AB的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次社会大课堂的数学实践活动中,王老师要求同学们测量教室窗户边框上的点C到地面的距离即CD的长,小英测量的步骤及测量的数据如下:
(1)在地面上选定点A, B,使点A,B,D在同一条直线上,测量出![]() 、
、![]() 两点间的距离为9米;
两点间的距离为9米;
(2)在教室窗户边框上的点C点处,分别测得点![]() ,
, ![]() 的俯角∠ECA=35°,∠ECB=45°.请你根据以上数据计算出
的俯角∠ECA=35°,∠ECB=45°.请你根据以上数据计算出![]() 的长.
的长.
(可能用到的参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com