
【题目】如图,在△ABC中,∠C=90°,把△ABC沿直线DE折叠,使△ADE与△BDE重合.
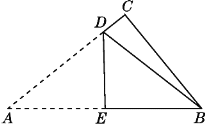
(1)若∠A=35°,则∠CBD的度数为________;
(2)若AC=8,BC=6,求AD的长;
(3)当AB=m(m>0),△ABC的面积为m+1时,求△BCD的周长.(用含m的代数式表示)
【答案】(1)∠CBD=20°;(2)AD=![]() ;(3) △BCD的周长为m+2
;(3) △BCD的周长为m+2
【解析】
(1)根据折叠可得∠1=∠A=35°,根据三角形内角和定理可以计算出∠ABC=55°,进而得到∠CBD=20°;
(2)根据折叠可得AD=DB,设CD=x,则AD=BD=8-x,再在Rt△CDB中利用勾股定理可得x2+62=(8-x)2,再解方程可得x的值,进而得到AD的长;
(3)根据三角形ACB的面积可得![]() ,
,
进而得到ACBC=2m+2,再在Rt△CAB中,CA2+CB2=BA2,再把左边配成完全平方可得CA+CB的长,进而得到△BCD的周长.
(1)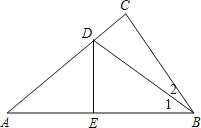
∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,
∴∠1=∠A=35°,
∵∠C=90°,
∴∠ABC=180°-90°-35°=55°,
∴∠2=55°-35°=20°,
即∠CBD=20°;
(2)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,
∴AD=DB,
设CD=x,则AD=BD=8-x,
在Rt△CDB中,CD2+CB2=BD2,
x2+62=(8-x)2,
解得:x= ![]() ,
,
AD=8-![]() =
=![]() ;
;
(3)∵△ABC 的面积为m+1,
∴![]() ACBC=m+1,
ACBC=m+1,
∴ACBC=2m+2,
∵在Rt△CAB中,CA2+CB2=BA2,
∴CA2+CB2+2ACBC=BA2+2ACBC,
∴(CA+BC)2=m2+4m+4=(m+2)2,
∴CA+CB=m+2,
∵AD=DB,
∴CD+DB+BC=m+2.
即△BCD的周长为m+2.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,![]() ,边
,边![]() 、
、![]() 都在
都在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() ,
,![]() .反比例函数
.反比例函数![]() 的图象经过点
的图象经过点![]() ,交
,交![]() 边于点
边于点![]() ,交
,交![]() 边于点
边于点![]() .
.

(1)分别求出点![]() 、
、![]() 的坐标;
的坐标;
(2)求以![]() 、
、![]() 、
、![]() 为顶点的
为顶点的![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
(1)如图①,若正方形![]() 的边长为6,点
的边长为6,点![]() 分别为边
分别为边![]() 上的点,且
上的点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() ;
;
问题探究:
(2)如图②,![]() ,
,![]() 是等腰直角三角形,顶点
是等腰直角三角形,顶点![]() 分别在
分别在![]() 的两边上,试说明点
的两边上,试说明点![]() 在
在![]() 的平分线上;
的平分线上;
问题解决:
(3)如图③,![]() ,
,![]() 是等边三角形,顶点
是等边三角形,顶点![]() 分别在
分别在![]() 的两边上,点
的两边上,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,求
,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,点
,点![]() 为
为![]() 三条角平分线的交点,
三条角平分线的交点,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() ,
,![]() ,则点
,则点![]() 到三边
到三边![]() 、
、![]() 、
、![]() 的距离为( )
的距离为( )
A. 2cm,2cm,2cm B. 3cm,3cm,3cm
C. 4cm,4cm,4cm D. 2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解初一年级学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了部分初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
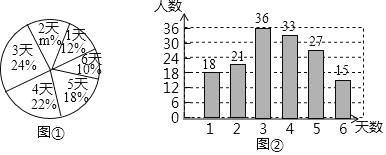
(I)本次随机抽样调查的学生人数为 ,图①中的m的值为 ;
(II)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(III)若该区初一年级共有学生2500人,请估计该区初一年级这个学期参加综合实践活动的天数大于4天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列结论一定成立的个数为
,则下列结论一定成立的个数为
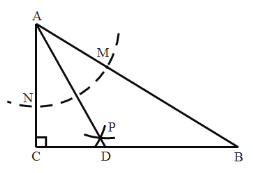
①![]() 是
是![]() 的平分线;
的平分线;
②若![]() ,则
,则![]() ;
;
③![]() ;
;
④点![]() 在
在![]() 的垂直平分线上.
的垂直平分线上.
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com