
【题目】抛物线![]() 的图像与
的图像与![]() 轴的一个交点为
轴的一个交点为![]() ,另一交点为
,另一交点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
(1)求该二次函数的表达式及顶点坐标;
(2)画出此二次函数的大致图象;利用图象回答:当![]() 取何值时,
取何值时,![]() ?
?
(3)若点![]() 在抛物线
在抛物线![]() 的图像上,且点
的图像上,且点![]() 到
到![]() 轴距离小于3,则
轴距离小于3,则![]() 的取值范围为 ;
的取值范围为 ;

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
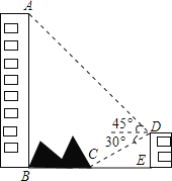
【题目】 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字﹣1,﹣2,3,现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M的所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
如图,将抛物线![]() 向右平移
向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度后,得到的抛物线
个单位长度后,得到的抛物线![]() ,平移后的抛物线
,平移后的抛物线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .抛物线
.抛物线![]() 的对称轴
的对称轴![]() 与抛物线
与抛物线![]() 交于点
交于点![]() .
.

(1)请你直接写出抛物线![]() 的解析式;(写出顶点式即可)
的解析式;(写出顶点式即可)
(2)求出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,AB=AC,点F在边BC上

(1)如图1,AF=BF,求证:AB2=BFBC;
(2)如图2,FC=2BF,点E、M在直线AB上,EF∥AC,cosB=n,且FM2=MEMB
①若M在边AB上,求![]() 的值(用含n的式子表示);
的值(用含n的式子表示);
②若M在BA的延长线上时,直接写出n的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
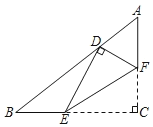
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则BD的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
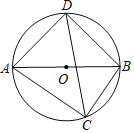
【题目】如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 分别在两个半圆上(不与点
分别在两个半圆上(不与点![]() 重合),
重合),![]() 的长分别是关于
的长分别是关于![]() 的方程
的方程![]()
![]() 的两个实数根.
的两个实数根.
(1)![]() 的值为_____;
的值为_____;
(2)连接![]() 三者之间的等量关系为_____.
三者之间的等量关系为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
在数学活动课上,老师出示了这样一个问题:如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的任意一点.将
边上的任意一点.将![]() 沿过点
沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在斜边
落在斜边![]() 上的点
上的点![]() 处.问是否存在
处.问是否存在![]() 是直角三角形?若不存在,请说明理由;若存在,求出此时
是直角三角形?若不存在,请说明理由;若存在,求出此时![]() 的长度.
的长度.

探究展示:勤奋小组很快找到了点![]() 、
、![]() 的位置.
的位置.
如图2,作![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,此时
,此时![]() 沿
沿![]() 所在的直线折叠,点
所在的直线折叠,点![]() 恰好在
恰好在![]() 上,且
上,且![]() ,所以
,所以![]() 是直角三角形.
是直角三角形.
问题解决:
(1)按勤奋小组的这种折叠方式,![]() 的长度为 .
的长度为 .
(2/span>)创新小组看完勤奋小组的折叠方法后,发现还有另一种折叠方法,请在图3中画出来.
(3)在(2)的条件下,求出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某浴室花洒实景图,图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度,离地面CD的距离BC=160cm.设花洒臂与墙面的夹角为α,可以扭动花洒臂调整角度,且花洒臂长AB=30cm.假设水柱AE垂直AB直线喷射,小华在离墙面距离CD=120cm处淋浴.

(1)当α=30°时,水柱正好落在小华的头顶上,求小华的身高DE.
(2)如果小华要洗脚,需要调整水柱AE,使点E与点D重合,调整的方式有两种:
①其他条件不变,只要把活动调节点B向下移动即可,移动的距离BF与小华的身高DE有什么数量关系?直接写出你的结论;
②活动调节点B不动,只要调整α的大小,在图3中,试求α的度数.
(参考数据:![]() ≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
≈1.73,sin8.6°≈0.15,sin36.9°≈0.60,tan36.9°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com