
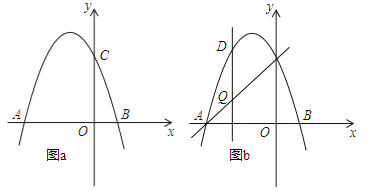
【题目】如图,抛物线![]() 交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).

(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
【答案】(1)![]() ;(2)P(﹣1,4),
;(2)P(﹣1,4),![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)把点A、C的坐标分别代入函数解析式,解方程组即可得到结论;
(2)设P点坐标为(x,![]() ),根据
),根据![]() 列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
(3)先求出直线AC的解析式为y=x+3,再设Q点坐标为(x,x+3),则D点坐标为(x,![]() ),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
(1)把A(﹣3,0),C(0,3)代入![]() ,得:
,得:![]() ,解得:
,解得:![]() ,故该抛物线的解析式为:
,故该抛物线的解析式为:![]() ;
;
(2)由(1)知,该抛物线的解析式为![]() ,则易得B(1,0),设P点坐标为(x,
,则易得B(1,0),设P点坐标为(x,![]() ),∵
),∵![]() ,∴
,∴![]() ,整理,得
,整理,得![]() 或
或![]() ,解得x=﹣1或x=
,解得x=﹣1或x=![]() ,则符合条件的点P的坐标为:(﹣1,4),
,则符合条件的点P的坐标为:(﹣1,4),![]() ,
,![]() ;
;
(3)设直线AC的解析式为![]() ,将A(﹣3,0),C(0,3)代入,得:
,将A(﹣3,0),C(0,3)代入,得:![]() ,解得:
,解得:![]() ,即直线AC的解析式为
,即直线AC的解析式为![]() .设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,
.设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,![]() ),QD=
),QD=![]() =
=![]() =
=![]() ,∴当x=
,∴当x=![]() 时,QD有最大值
时,QD有最大值![]() .
.


科目:初中数学 来源: 题型:
【题目】定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若![]() ,则称点D是△ABC中BC边上的“好点”.
,则称点D是△ABC中BC边上的“好点”.
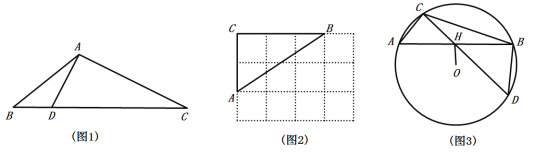
(1)如图2,△ABC的顶点是![]() 网格图的格点,请仅用直尺画出AB边上的一个“好点”.
网格图的格点,请仅用直尺画出AB边上的一个“好点”.
(2)△ABC中,BC=9,![]() ,
,![]() ,点D是BC边上的“好点”,求线段BD的长.
,点D是BC边上的“好点”,求线段BD的长.
(3)如图3,△ABC是![]() 的内接三角形,OH⊥AB于点H,连结CH并延长交
的内接三角形,OH⊥AB于点H,连结CH并延长交![]() 于点D.
于点D.
①求证:点H是△BCD中CD边上的“好点”.
②若![]() 的半径为9,∠ABD=90°,OH=6,请直接写出
的半径为9,∠ABD=90°,OH=6,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
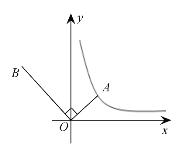
【题目】如图,已知点A是反比例函数 y = ![]() (x>0 )的图象上的一个动点,连接OA ,OB⊥OA,且OB =2OA.那么经过点B的反比例函数的表达式为( )
(x>0 )的图象上的一个动点,连接OA ,OB⊥OA,且OB =2OA.那么经过点B的反比例函数的表达式为( )
A.y=-![]() B.y=
B.y= ![]() C.y=-
C.y=-![]() D.y=
D.y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张分别标有数字![]() 、
、![]() 、
、![]() 的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为
的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为![]() (不放回),再从中任意抽取一张,将上面的数字记为
(不放回),再从中任意抽取一张,将上面的数字记为![]() ,这样的数字
,这样的数字![]() ,
,![]() 能使关于
能使关于![]() 的一元二次方程
的一元二次方程![]() 有两个正根的概率为________.
有两个正根的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市实验中学计划在暑假第二周的星期一至星期五开展暑假社会实践活动,要求每位学生选择两天参加活动.
(1)甲同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)乙同学随机选择两天,其中有一天是星期三的概率是多少?(列表或画树形图或列举)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:如图,AD为⊙O的直径。
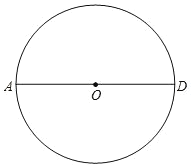
(1)求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);
(2)已知连接DF,⊙O的半径为4,求DF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.

(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com