
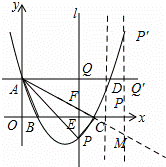
如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当0<t≤8时,求△AP C面积的最大值;
C面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值; 若不存在,请说明理由.
若不存在,请说明理由.
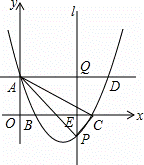
解:(1)由题意知x1、x2是方程mx2﹣8mx+4m+2=0的两根,
∴x1+x2=8,
由
解得: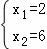
∴B(2,0)、C(6,0)
则4m﹣16m+4m+2=0,
解得:m=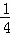 ,
,
∴该抛物线解析式为:y= ;
;
(2)可求得A(0,3)
设直线AC的解析式为:y=kx+b,
∵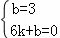
∴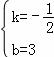
∴直线AC的解析式为:y=﹣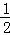 x+3,
x+3,
要构成△APC,显然t≠6,分两种情况讨论:
①当0<t<6时,设直线l与AC交点为F,则:F(t,﹣ ),
),
∵P(t, ),∴PF=
),∴PF=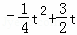 ,
,
∴S△APC=S△APF+S△CPF
=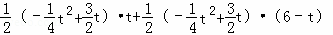
=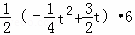
=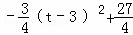 ,
,
此时最大值为: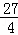 ,
,
②当6≤t≤8时,设直线l与AC交点为M,则:M(t,﹣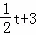 ),
),
∵P(t, ),∴PM=
),∴PM= ,
,
∴S△APC=S△APF﹣S△CPF=
=
= ,
,
当t=8时,取最大值,最大值为:12,
综上可知,当0<t≤8时,△APC面积的最大值为12;
(3)如图,连接AB,则△AOB中,∠AOB=90°,AO=3,BO=2,
Q(t,3),P(t,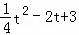 ),
),
①当2<t≤6时,AQ=t,PQ=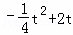 ,
,
若:△AOB∽△AQP,则: ,
,
即: ,
,
∴t=0(舍),或t=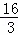 ,
,
若△AOB∽△PQA,则: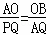 ,
,
即: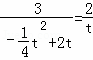 ,
,
∴t=0(舍)或t=2(舍),
②当t>6时,AQ′=t,PQ′=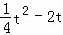 ,
,
若:△AOB∽△AQP,则: ,
,
即: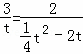 ,
,
∴t=0(舍),或t=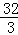 ,
,
若△AOB∽△PQA,则: ,
,
即: ,
,
∴t=0(舍)或t=14,
∴t= 或t=
或t= 或t=14.
或t=14.


科目:初中数学 来源: 题型:
下列四个命题中,真命题是( )
|
| A. | “任意四边形内角和为360°”是不可能事件 |
|
| B. | “湘潭市明天会下雨”是必然事件 |
|
| C. | “预计本题的正确率是95%”表示100位考生中一定有95人做对 |
|
| D. | 抛掷一枚质地均匀的硬币,正面朝上的概率是 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=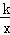 (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
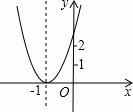
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元.(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
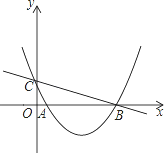
如图,已知抛物线y=ax2﹣5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)若点N是抛物线上的动点,过点N作NH⊥x轴,垂足为H,以B,N,H为顶点的三角形是否能够与△OBC相似?若能,请求出所有符合条件的点N的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com