
【题目】甲乙两名战士在相同条件下各射击10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7 乙:6,7,7,6,7,8,7,9,8,5
(1)分别求出两组数据的方差和标准差;
(2)根据计算结果,评价一下两名战士的射击情况.
【答案】(1)![]() ,
,![]() ;
;![]() ,
,![]() ;(2)平均水平相同,乙射击较稳定
;(2)平均水平相同,乙射击较稳定
【解析】
(1)先求出甲和乙的平均数,再根据方差公式和标准差公式进行计算即可;
(2)依据甲乙两人平均成绩一样,乙射击成绩的方差小于甲,即可得出乙的成绩更加稳定.
解(1)∵![]() =
=![]() ×(8+6+7+8+6+5+9+10+4+7)=7,
×(8+6+7+8+6+5+9+10+4+7)=7,
∴![]() =
=![]() ×[(87)2+(67)2+(77)2+(87)2+(6-7)2+(57)2+(97)2+(107)2+(47)2+(77)2],
×[(87)2+(67)2+(77)2+(87)2+(6-7)2+(57)2+(97)2+(107)2+(47)2+(77)2],
=![]() ×(1+1+0+1+1+4+4+9+9+0),
×(1+1+0+1+1+4+4+9+9+0),
=3,
∴![]() ;
;
∵![]() =
=![]() ×(6+7+7+6+7+8+7+9+8+5)=7,
×(6+7+7+6+7+8+7+9+8+5)=7,
∴![]() =
=![]() ×[(67)2+(77)2+(77)2+(67)2+(7-7)2+(87)2+(77)2+(97)2+(87)2+(57)2],
×[(67)2+(77)2+(77)2+(67)2+(7-7)2+(87)2+(77)2+(97)2+(87)2+(57)2],
=![]() ×(1+0+0+1+0+1+0+4+1+4),
×(1+0+0+1+0+1+0+4+1+4),
=![]() ,
,
∴![]() ;
;
(2)∵![]() =
=![]() ,
,![]() <
<![]() ,
,
∴甲乙两人平均成绩一样,乙射击成绩的方差小于甲,即可得出乙的成绩更加稳定.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
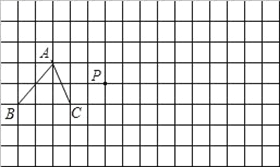
【题目】在下面16×8的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出:
(1)△ABC的中心对称图形,A点为对称中心;
(2)△ABC关于点P的位似△A′B′C′,且位似比为1:2;
(3)以A、B、C、D为顶点的所有格点平行四边形ABCD的顶点D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新知认识:在△ABC中,∠A,∠B,∠C所对的边分别用a,b,c表示,如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.
(1)特殊验证:如图1,在△ABC中,若a=![]() ,b=1,c=2,求证:△ABC为倍角三角形;
,b=1,c=2,求证:△ABC为倍角三角形;
(2)模型探究:如图2,对于任意的倍角三角形,若∠A=2∠B,求证:a2=b(b+c)
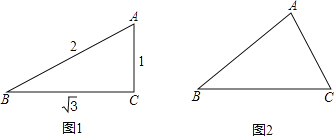
查看答案和解析>>
科目:初中数学 来源: 题型:
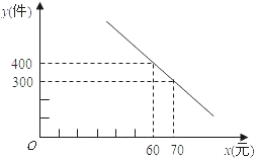
【题目】某服装公司试销一种成本为每件50元的T恤衫,规定试销时的销售单价不低于成本价,又不高于每件70元,试销中销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)求y与x之间的函数关系式;
(2)设公司获得的总利润(总利润=总销售额-总成本)为P元,求P与x之间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一根长22cm的铁丝,
(1)能否围成面积是30cm2的矩形?如果能,求出矩形的边长,如果不能说明理由;
(2)能否围成面积是32cm2的矩形?如果能,求出矩形的边长,如果不能说明理由;
(3)请探索能围成的矩形面积的最大值是多少 cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)求一次函数![]() 的表达式;
的表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
①cos(α+β)=cosαcosβ﹣sinαsinβ;sin(α+β)=sinαcosβ+cosαsinβ;
②tan(α+β)=![]() .
.
③利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如tan105°=tan(45°+60°)=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
(1)求cos75°的值;
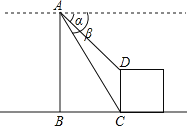
(2)如图,直升机在一建筑物CD上方的点A处测得建筑物顶端点D的俯角α为60°,底端点C的俯角β为75°,此时直升机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)
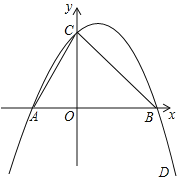
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若P是抛物线上一点,且S△ABP=![]() S△ABC,这样的点P有几个请直接写出它们的坐标.
S△ABC,这样的点P有几个请直接写出它们的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
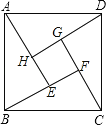
【题目】如图,这个图案是3世纪我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.已知AE=3,BE=2,若向正方形ABCD内随意投掷飞镖(每次均落在正方形ABCD内,且落在正方形ABCD内任何一点的机会均等),则恰好落在正方形EFGH内的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com