
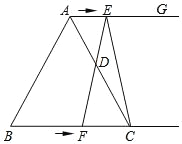
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;
②当t为 s时,△ACE的面积是△ACF的面积的2倍.
【答案】(1)证明见解析;(2)①8;②![]() 或
或![]() .
.
【解析】
(1)判断出△ADE≌△CDF得出AE=CF,即可得出结论;
(2)①先求出AC=BC=8,进而判断出AE=CF=AC=8,即可得出结论;
②先判断出△ACE和△ACF的边AE和CF上的高相等,进而判断出AE=2CF,再分两种情况,建立方程求解即可得出结论.
解:(1)如图1.
∵AG∥BC,
∴∠EAC=∠FCA,∠AED=∠CFD.
∵EF经过AC边的中点D,
∴AD=CD,
∴△ADE≌△CDF(AAS),
∴AE=CF.
∵AE∥FC,
∴四边形AFCE是平行四边形;
(2)①如图2.
∵△ABC是等边三角形,
∴AC=BC=8.
∵四边形ACFE是菱形,
∴AE=CF=AC=BC=8,且点F在BC延长线上,由运动知,AE=t,BF=2t,
∴CF=2t﹣8,t=8,将t=8代入CF=2t﹣8中,
得CF=8=AC=AE,符合题意,即:t=8秒时,四边形ACFE是菱形.
故答案为:8;
②设平行线AG与BC的距离为h,
∴△ACE边AE上的高为h,△ACF的边CF上的高为h.
∵△ACE的面积是△ACF的面积的2倍,
∴AE=2CF,当点F在线段BC上时(0<t<4),CF=8﹣2t,AE=t,
∴t=2(8﹣2t),
∴![]()
当点F在BC的延长线上时(t>4),CF=2t﹣8,AE=t,
∴t=2(2t﹣8),
∴![]()
即:t=![]() 秒或
秒或![]() 秒时,△ACE的面积是△ACF的面积的2倍.
秒时,△ACE的面积是△ACF的面积的2倍.
故答案为:![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
【题目】有3张正面分别写有数字![]() ,0,1的卡片,它们的背面完全相同,现将这3张卡片背面朝上洗匀,小明先从中任意抽出一张卡片记下数字为x;小亮再从剩下的卡片中任意取出一张记下数字为y,记作
,0,1的卡片,它们的背面完全相同,现将这3张卡片背面朝上洗匀,小明先从中任意抽出一张卡片记下数字为x;小亮再从剩下的卡片中任意取出一张记下数字为y,记作![]() .
.
![]() 用列表或画树状图的方法列出所有可能的点P的坐标;
用列表或画树状图的方法列出所有可能的点P的坐标;
![]() 若规定:点
若规定:点![]() 在第二象限小明获胜;点
在第二象限小明获胜;点![]() 在第四象限小亮获胜,游戏规则公平吗?
在第四象限小亮获胜,游戏规则公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某项工程由甲乙两队合作12天可以完成,供需工程费用13800元,乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多150元。
(1)甲乙两队单独完成这项工程分别需要多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成这项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
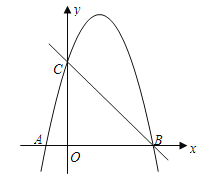
(1)求抛物线的解析式;
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,把![]() 和
和![]() 按图1摆放,
按图1摆放,![]() 点C与E点重合
点C与E点重合![]() ,点B、C、E、F始终在同一条直线上,
,点B、C、E、F始终在同一条直线上,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图2,
,如图2,![]() 从图1的位置出发,以每秒1个单位的速度沿CB方向匀速移动,同时,点P从A出发,沿AB以每秒1个单位向点B匀速移动,AC与
从图1的位置出发,以每秒1个单位的速度沿CB方向匀速移动,同时,点P从A出发,沿AB以每秒1个单位向点B匀速移动,AC与![]() 的直角边相交于Q,当P到达终点B时,
的直角边相交于Q,当P到达终点B时,![]() 同时停止运动连接PQ,设移动的时间为
同时停止运动连接PQ,设移动的时间为![]() 解答下列问题:
解答下列问题:
![]() 在平移的过程中,当点D在
在平移的过程中,当点D在![]() 的AC边上时,求AB和t的值;
的AC边上时,求AB和t的值;
![]() 在移动的过程中,是否存在
在移动的过程中,是否存在![]() 为等腰三角形?若存在,求出t的值;若不存在,说明理由.
为等腰三角形?若存在,求出t的值;若不存在,说明理由.
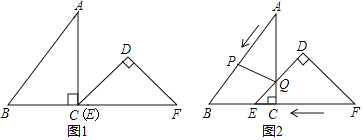
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象在第一象限内的交点为
的图象在第一象限内的交点为![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 在x轴上是否存在点P,使
在x轴上是否存在点P,使![]() ?若存在,求出点P的坐标;若不存在,说明理由.
?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A.①② B.①④ C.①③④ D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com