
分析 (1)要想证明对于任意实数k,方程有两个不相等的实数根,只要证明△>0即可;
(2)把方程的一根代入原方程求出a的值,然后把a的值代入原方程求出方程的另一个根.
解答 解:(1)∵2-ax+a=1,
∴2-ax+a-1=0,
∴△=a2-4×1×(a-1)=a2-4a+4=(a-2)2,
∵(a-2)2≥0,
∴对于任意实数a,方程总有实数根
(2)把x=3代入原方程,得a=4.
把a=4代入原方程,得x2-4x+3=0.
∴x1=3,x2=1.
∴方程的另一个根是1.
点评 本题考查了一元二次方程根的判别式以及解一元二次方程的方法,一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


科目:初中数学 来源: 题型:解答题
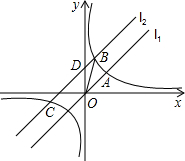 如图,直线l1:y=x与反比例函数$y=\frac{k}{x}$的图象c相交于点A(2,a),将直线l1向上平移3个单位长度得到l2,直线l2与c相交于B,C两点,(点B在第一象限),交y轴于点D.
如图,直线l1:y=x与反比例函数$y=\frac{k}{x}$的图象c相交于点A(2,a),将直线l1向上平移3个单位长度得到l2,直线l2与c相交于B,C两点,(点B在第一象限),交y轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
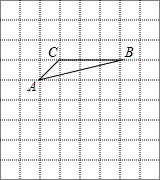 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
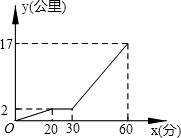 星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )| A. | 小强从家到公共汽车站步行了2千米 | |
| B. | 小强在公共汽车站等小明用了10分钟 | |
| C. | 公交车的平均速度是34千米/小时 | |
| D. | 小强乘公交车用了30分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-1 | B. | x≠-3 | C. | x≥-1且x≠-3 | D. | x<-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=4,n=32 | B. | m=4,n=-32 | C. | m=-4,n=32 | D. | m=-4,n=-32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com