
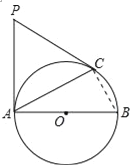
【题目】已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
(1)求∠P的大小;
(2)若AB=6,求PA的长.

【答案】(1)∠P=60°;(2)![]() .
.
【解析】
试题分析:(1)由圆的切线的性质,得∠PAB=90°,结合∠BAC=30°得∠PAC=90°﹣30°=60°.由切线长定理得到PA=PC,得△PAC是等边三角形,从而可得∠P=60°.
(2)连接BC,根据直径所对的圆周角为直角,得到∠ACB=90°,结合Rt△ACB中AB=6且∠BAC=30°,得到AC=ABcos∠BAC=![]() .最后在等边△PAC中,可得PA=AC=
.最后在等边△PAC中,可得PA=AC=![]() .
.
试题解析:(1)∵PA是⊙O的切线,AB为⊙O的直径,∴PA⊥AB,即∠PAB=90°.
∵∠BAC=30°,∴∠PAC=90°﹣30°=60°.
又∵PA、PC切⊙O于点A、C,∴PA=PC,∴△PAC是等边三角形,∴∠P=60°;
(2)如图,连接BC.
∵AB是直径,∠ACB=90°,∴在Rt△ACB中,AB=6,∠BAC=30°,可得AC=ABcos∠BAC=6×cos30°=![]() .
.
又∵△PAC是等边三角形,∴PA=AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:计算:(﹣5)÷( ![]() ﹣
﹣ ![]() )×20 解:原式=(﹣5)÷(﹣
)×20 解:原式=(﹣5)÷(﹣ ![]() )×20 (第一步)
)×20 (第一步)
=(﹣5)÷(﹣4)(第二步)
=﹣20 (第三步)
(1)上述解题过程中有两处错误, 第一处是第步,错误的原因是;
第二处是第步,错误的原因是;
(2)把正确的解题过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
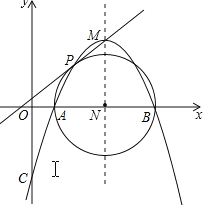
【题目】如图,已知抛物线![]() 的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:![]() (
(![]() ),并指出顶点M的坐标;
),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”是(1,2)的点的个数共有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
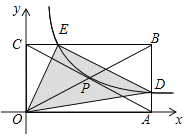
【题目】如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数![]() (x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:先化简,再求值
(1)先化简,再求值:x2﹣(x+2)(2﹣x)﹣2(x﹣5)2 , 其中x=3.
(2)解不等式组 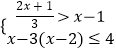 ,并求它的整数解.
,并求它的整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②); 再沿过D点的直线折叠, 使得 C点落在DA边上的点N处, E点落在AE边上的点M处,折痕为 DG(如图).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD的长与宽的比值为( )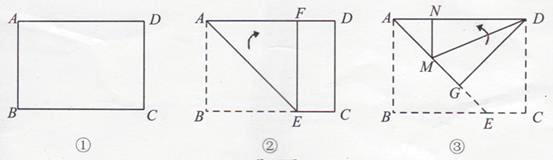
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com