
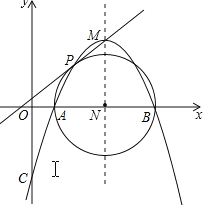
【题目】如图,已知抛物线![]() 的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:![]() (
(![]() ),并指出顶点M的坐标;
),并指出顶点M的坐标;
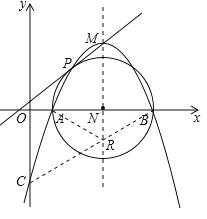
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
【答案】(1)![]() ,M(
,M(![]() ,
,![]() );(2)
);(2)![]() ,(
,(![]() ,
,![]() );(3)证明见试题解析.
);(3)证明见试题解析.
【解析】
试题分析:(1)利用配方法把一般式转化为顶点式,然后根据二次函数的性质求出抛物线的顶点坐标;
(2)连接BC,则BC与对称轴的交点为R,此时CR+AR的值最小;先求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,进而求出其最小值和点R的坐标;
(3)设点P坐标为(x,![]() ).根据NP
).根据NP![]() AB=
AB=![]() ,列出方程
,列出方程![]() ,解方程得到点P坐标,再计算得出
,解方程得到点P坐标,再计算得出![]() ,由勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.
,由勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.
试题解析:(1)∵![]() =
=![]() ,∴抛物线的解析式化为顶点式为:
,∴抛物线的解析式化为顶点式为:![]() ,顶点M的坐标是(
,顶点M的坐标是(![]() ,
,![]() );
);
(2)∵![]() ,∴当y=0时,
,∴当y=0时,![]() ,解得x=1或6,∴A(1,0),B(6,0),∵x=0时,y=﹣3,∴C(0,﹣3).连接BC,则BC与对称轴x=
,解得x=1或6,∴A(1,0),B(6,0),∵x=0时,y=﹣3,∴C(0,﹣3).连接BC,则BC与对称轴x=![]() 的交点为R,连接AR,则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,最小值为BC=
的交点为R,连接AR,则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,最小值为BC=![]() =
=![]() .设直线BC的解析式为
.设直线BC的解析式为![]() ,∵B(6,0),C(0,﹣3),∴
,∵B(6,0),C(0,﹣3),∴![]() ,解得:
,解得: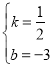 ,∴直线BC的解析式为:
,∴直线BC的解析式为:![]() ,令x=
,令x=![]() ,得y=
,得y=![]() =
=![]() ,∴R点坐标为(
,∴R点坐标为(![]() ,
,![]() );
);
(3)设点P坐标为(x,![]() ).∵A(1,0),B(6,0),∴N(
).∵A(1,0),B(6,0),∴N(![]() ,0),∴以AB为直径的⊙N的半径为
,0),∴以AB为直径的⊙N的半径为![]() AB=
AB=![]() ,∴NP=
,∴NP=![]() ,即
,即![]() ,移项得,
,移项得,![]() ,得:
,得:![]() ,整理得:
,整理得:![]() ,解得
,解得![]() (与A重合,舍去),
(与A重合,舍去),![]() ,
,![]() (在对称轴的右侧,舍去),
(在对称轴的右侧,舍去),![]() (与B重合,舍去),∴点P坐标为(2,2).∵M(
(与B重合,舍去),∴点P坐标为(2,2).∵M(![]() ,
,![]() ),N(
),N(![]() ,0),∴
,0),∴![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,∴
,∴![]() ,∴∠MPN=90°,∵点P在⊙N上,∴直线MP是⊙N的切线.
,∴∠MPN=90°,∵点P在⊙N上,∴直线MP是⊙N的切线.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=﹣ ![]() x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC
x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC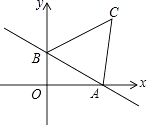
(1)求△ABC的面积和点C的坐标;
(2)如果在第二象限内有一点P(a, ![]() ),试用含a的代数式表示四边形ABPO的面积.
),试用含a的代数式表示四边形ABPO的面积.
(3)在x轴上是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 选举中,人们通常最关心的数据是众数
B. 数据6、4、2、2、1的平均数是3
C. 数据3、5、4、1、-2的中位数是3
D. “打开电视机,中央一套正在播广告”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
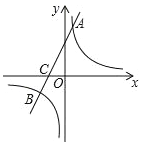
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴的原点为O,如图所示,点A表示﹣2,点B表示3,请回答下列问题:
(1)数轴是什么图形?数轴在原点右边的部分(包括原点)是什么图形?数轴上表示不小于﹣2,且不大于3的部分是什么图形?请你分别给它们取一个合适的名字;
(2)请你在射线AO上再标上一个点C(不与A点重合),那么表示点C的值x的取值范围 .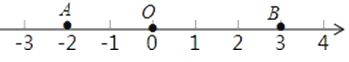
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是 .
MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是 . 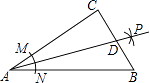
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com