
【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是 .
MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是 . 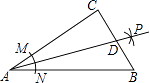
科目:初中数学 来源: 题型:
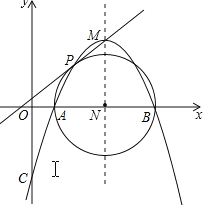
【题目】如图,已知抛物线![]() 的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:![]() (
(![]() ),并指出顶点M的坐标;
),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:先化简,再求值
(1)先化简,再求值:x2﹣(x+2)(2﹣x)﹣2(x﹣5)2 , 其中x=3.
(2)解不等式组 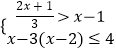 ,并求它的整数解.
,并求它的整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分住校生放学后到学校开水房打水,每人接水2升,他们先同时打开两个放水龙头,后来因故障关闭一个放水龙头,假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量m(升)与接水时间t(分)的函数关系图象如图所示,请结合图象,回答下列问题: 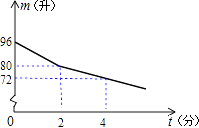
(1)请直接写出m与t之间的函数关系式: .
(2)前15位同学接水结束共需要几分钟?
(3)小敏说“今天我们寝室的8位同学去开水房连续接完水恰好用了3分钟.”你说可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,是由一些棱长为单位 1 的相同的小正方体组合成的简单几何体.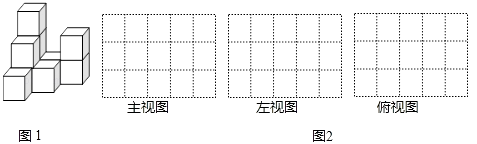
(1)请在图 2 方格纸中分别画出几何体的主视图、左视图和俯视图.
(2)如果在其表面涂漆,则要涂平方单位.(几何体放在地上,底面无法涂上漆)
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 AB,CD 相交于点 O,OE 平分∠AOD,OF⊥OC,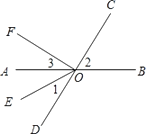
(1)图中∠AOF 的余角是(把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据 , 可得∠BOD=度;
(3)如果∠1=32°,求∠2 和∠3 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②); 再沿过D点的直线折叠, 使得 C点落在DA边上的点N处, E点落在AE边上的点M处,折痕为 DG(如图).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD的长与宽的比值为( )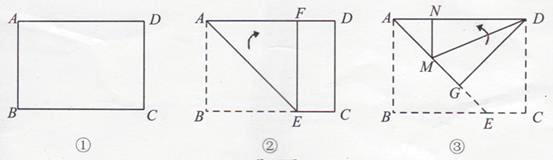
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中最适合普遍调查的是( )
A.调查某品牌灯泡的使用寿命B.调查振兴区居民网上购物情况
C.调查锦江山上各种鸟的总数量D.调查我国大型客机C919的零件质量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com