
【题目】已知数轴的原点为O,如图所示,点A表示﹣2,点B表示3,请回答下列问题:
(1)数轴是什么图形?数轴在原点右边的部分(包括原点)是什么图形?数轴上表示不小于﹣2,且不大于3的部分是什么图形?请你分别给它们取一个合适的名字;
(2)请你在射线AO上再标上一个点C(不与A点重合),那么表示点C的值x的取值范围 .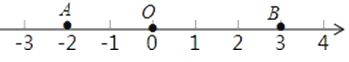
科目:初中数学 来源: 题型:
【题目】下列问题,适合抽样调查的是( )
A. 了解一批灯泡的使用寿命 B. 学校招聘老师,对应聘人员的面试
C. 了解全班学生每周体育锻炼时间 D. 上飞机前对旅客的安检
查看答案和解析>>
科目:初中数学 来源: 题型:
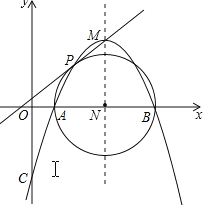
【题目】如图,已知抛物线![]() 的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:![]() (
(![]() ),并指出顶点M的坐标;
),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
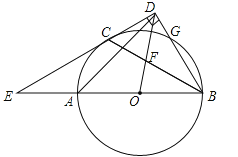
【题目】如图,AB是⊙O的直径,C,G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线.
(2)若![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1,l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”是(1,2)的点的个数共有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
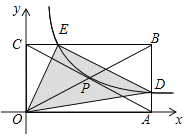
【题目】如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数![]() (x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:先化简,再求值
(1)先化简,再求值:x2﹣(x+2)(2﹣x)﹣2(x﹣5)2 , 其中x=3.
(2)解不等式组 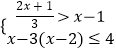 ,并求它的整数解.
,并求它的整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 AB,CD 相交于点 O,OE 平分∠AOD,OF⊥OC,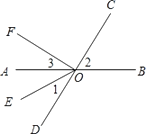
(1)图中∠AOF 的余角是(把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据 , 可得∠BOD=度;
(3)如果∠1=32°,求∠2 和∠3 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com