
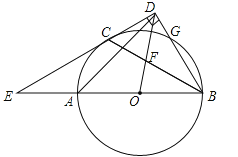
【题目】如图,AB是⊙O的直径,C,G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线.
(2)若![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD=![]() ,求AD的长.
,求AD的长.
【答案】(1)证明见试题解析;(2)30°;(3)![]() .
.
【解析】
试题分析:(1)如图1,连接OC,AC,CG,则有∠ABC=∠CBG,根据同圆的半径相等得到OC=OB,于是得到∠OCB=∠OBC,由等量代换得到∠OCB=∠CBG,根据平行线的判定得到OC∥BG,即可得到结论;
(2)由OC∥BD,得到△OCF∽△BDF,△EOC∽△EBD,得到![]() ,
,![]() ,根据直角三角形的性质即可得到结论;
,根据直角三角形的性质即可得到结论;
(3)如图2,过A作AH⊥DE于H,解直角三角形得到BD,DE,BE,在Rt△DAH中,用勾股定理即可得到AD的长.
试题解析:(1)如图1,连接OC,AC,CG,∵AC=CG,∴![]() ,∴∠ABC=∠CBG,∵OC=OB,∴∠OCB=∠OBC,∴∠OCB=∠CBG,∴OC∥BG,∵CD⊥BG,∴OC⊥CD,∴CD是⊙O的切线;
,∴∠ABC=∠CBG,∵OC=OB,∴∠OCB=∠OBC,∴∠OCB=∠CBG,∴OC∥BG,∵CD⊥BG,∴OC⊥CD,∴CD是⊙O的切线;
(2)∵OC∥BD,∴△OCF∽△BDF,△EOC∽△EBD,∴![]() ,∴
,∴![]() ,∵OA=OB,∴AE=OA=OB,∴OC=
,∵OA=OB,∴AE=OA=OB,∴OC=![]() OE,∵∠ECO=90°,∴∠E=30°;
OE,∵∠ECO=90°,∴∠E=30°;
(3)如图2,过A作AH⊥DE于H,∵∠E=30°,∴∠EBD=60°,∴∠CBD=![]() ∠EBD=30°,∵CD=
∠EBD=30°,∵CD=![]() ,∴BD=3,DE=
,∴BD=3,DE=![]() ,BE=6,∴AE=
,BE=6,∴AE=![]() BE=2,∴AH=1,∴EH=
BE=2,∴AH=1,∴EH=![]() ,∴DH=
,∴DH=![]() ,在Rt△DAH中,AD=
,在Rt△DAH中,AD=![]() =
=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( ) 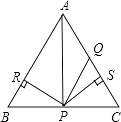
A.全部正确
B.仅①和③正确
C.仅①正确
D.仅①和②正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在计算学期平均分的时候按照如下标准,作业占10%,测验占20%,期中考试占30%,期末考试占40%,小丽的成绩如表所示,则小丽的平均分是________分.
学生 | 作业 | 测验 | 期中考试 | 期未考试 |
小丽 | 80 | 75 | 70 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 选举中,人们通常最关心的数据是众数
B. 数据6、4、2、2、1的平均数是3
C. 数据3、5、4、1、-2的中位数是3
D. “打开电视机,中央一套正在播广告”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴的原点为O,如图所示,点A表示﹣2,点B表示3,请回答下列问题:
(1)数轴是什么图形?数轴在原点右边的部分(包括原点)是什么图形?数轴上表示不小于﹣2,且不大于3的部分是什么图形?请你分别给它们取一个合适的名字;
(2)请你在射线AO上再标上一个点C(不与A点重合),那么表示点C的值x的取值范围 .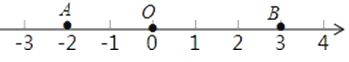
查看答案和解析>>
科目:初中数学 来源: 题型:
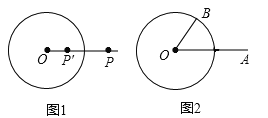
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=![]() ,则称点P′是点P关于⊙O的“反演点”.
,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读填空:请你阅读芳芳的说理过程并填出理由:
(1)如图1,已知AB∥CD.
求证:∠BAE+∠DCE=∠AEC.
理由:作EF∥AB,则有EF∥CD()
∴∠1=∠BAE,∠2=∠DCE()
∴∠AEC=∠1+∠2=∠BAE+∠DCE()
思维拓展: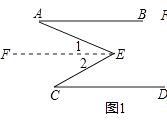
(2)如图2,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.BE、DE所在直线交于点E,若∠FAE=m°,∠ABC=n°,求∠BED的度数.(用含m、n的式子表示)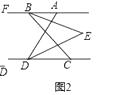
(3)将图2中的线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,得到图3,直接写出∠BED的度数是(用含m、n的式子表示).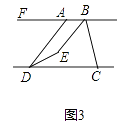
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数![]() 和反比例函数
和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出方程![]() 的解;
的解;
(3)求△AOB的面积;
(4)观察图象,直接写出不等式![]() 的解集.
的解集.
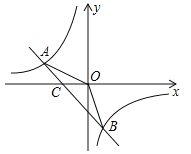
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com