
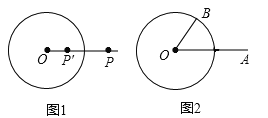
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=![]() ,则称点P′是点P关于⊙O的“反演点”.
,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E. 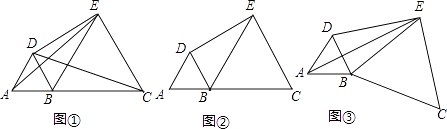
(1)如图①,连结CD,AE,求证:CD=AE;
(2)如图②,若AB=1,BC=2,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入表示它所在的集合里.
﹣2,7,﹣1.732,0,3.14,﹣(+5),﹣ ![]() ,﹣(﹣3),2007
,﹣(﹣3),2007
(1)正数集合{ …}
(2)负数集合{ …}
(3)整数集合{ …}
(4)有理数集合{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
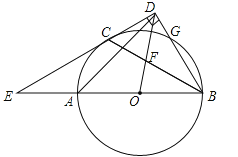
【题目】如图,AB是⊙O的直径,C,G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
(1)求证:CD是⊙O的切线.
(2)若![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 . 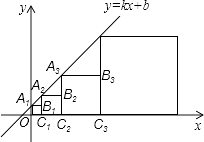
查看答案和解析>>
科目:初中数学 来源: 题型:
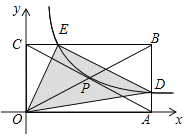
【题目】如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数![]() (x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
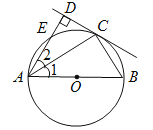
【题目】(满分10分)如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
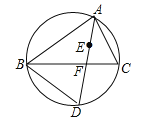
【题目】如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
(1)求证:△BFD∽△ABD;
(2)求证:DE=DB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com