如图，小俊在A处利用高为1.8米的测角仪AB测得楼EF顶部E的仰角为30°，然后前进12米到达C处，又测得楼顶E的仰角为60°，求楼EF的高度．（结果精确到0.1米）（参考数据：
=1.414，
=1.732）
【考点】解直角三角形的应用-仰角俯角问题．
【分析】设楼EF的高为x米，根据正切的概念用x表示出DG、BG，根据题意列出方程，解方程即可．
【解答】解：设楼EF的高为x米，则EG=EF﹣GF=（x﹣1.8）米，
由题意得：EF⊥AF，DC⊥AF，BA⊥AF，BD⊥EF，
在Rt△EGD中，DG=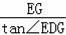
=
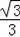
（x﹣1.8），
在Rt△EGB中，BG=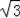
（x﹣1.8），
∴CA=DB=BG﹣DG=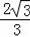
（x﹣1.8），
∵CA=12米，
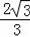
∴（x﹣1.8）=12，
解得：x=6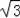
+1.8≈12.2，
答：楼EF的高度约为12.2米．
【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题，正确理解仰角和俯角的概念、熟记锐角三角函数的定义是解题的关键．
快捷英语周周练系列答案科目：初中数学 来源： 题型：
图1是小明在健身器材上进行仰卧起坐锻炼时情景．图2是小明锻炼时上半身由EM位置运动到与地面垂直的EN位置时的示意图．已知BC=0.64米，AD=0.24米，α=18°．（sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）
（1）求AB的长（精确到0.01米）；
（2）若测得EN=0.8米，试计算小明头顶由M点运动到N点的路径弧MN的长度（结果保留π）
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，已知：如图，在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y=
（x＞0）经过D点，交BC的延长线于E点，且OB•AC=160，有下列四个结论：
①双曲线的解析式为y=
（x＞0）；②E点的坐标是（5，8）；③sin∠COA=
；④AC+OB=12
．其中正确的结论有（ ）
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
2011年北京春季房地产展示交易会期间，某公司对参加本次房交会的消费者的年收入和打算购买住房面积这两项内容进行了随机调查，共发放100份问卷，并全部收回．统计相关数据后，制成了如下的统计表和统计图：
消费者年收入统计表
| 年收入（万元） | 4.8 | 6 | 9 | 12 | 24 |
| 被调查的消费者数（人） | 10 | 50 | 30 | 9 | 1 |
请你根据以上信息，回答下列问题：
（1）补全统计表和统计图；
（2）打算购买住房面积小于100平方米的消费者人数占被调查人数的百分比为 ；
（3）求被调查的消费者平均每人年收入为多少万元？
查看答案和解析>>
科目：初中数学 来源： 题型：
嘉淇想证明三角形内角和是180°和其他一些的命题．请完成下列一些命题和证明．
（1）怎样证明三角形内角和是180°呢？
（2）已知命题：等腰三角形底边上的中线和顶角的角平分线重合，证明这个命题，并写出它的逆命题，逆命题成立吗？
命题： 底边上的中线和顶角的角平分线重合的三角形是等腰三角形
证明： 证明：在△ABD和△ACD中，
∵
，
∴△ABD≌△ACD（SSS），
∴∠BAD=∠CAD
由此我们不难发现： 此命题是互逆命题
那么怎样证明呢？请写出证明过程．（可以画出作图痕迹．）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
+|1﹣4sin60°|+（2016π﹣
）0．
B．
C．
