
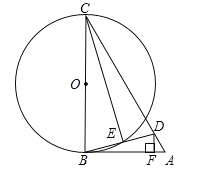
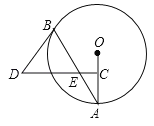
【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作⊙O,交BD于点E,连接CE,过D作DF⊥AB于点F,∠BCD=2∠ABD.
(1)求证:AB是⊙O的切线;
(2)若∠A=60°,DF=![]() ,求⊙O的直径BC的长.
,求⊙O的直径BC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由CD=CB,∠BCD=2∠ABD,可证得∠BCE=∠ABD,继而求得∠ABC=90°,则可证得AB是⊙O的切线;
(2)由∠A=60°,DF=![]() ,可求得AF、BF的长,易证得△ADF∽△ACB,然后由相似三角形的对应边成比例,求得答案.
,可求得AF、BF的长,易证得△ADF∽△ACB,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)证明:∵CD=CB,∴∠CBD=∠CDB,∵AB是⊙O的直径,∴∠CBE=90°,∴∠CBD+∠BCE=∠CDB+∠DCE,∴∠BCE=∠DCE,即∠BCD=2∠BCE,∵∠BCD=2∠ABD,∴∠ABD=∠BCE,∴∠CBD+∠ABD=∠CBD+∠BCE=90°,∴CB⊥AB,∵CB为直径,∴AB是⊙O的切线;
(2)∵∠A=60°,DF=![]() ,∴在Rt△AFD中,AF=
,∴在Rt△AFD中,AF=![]() =
=![]() =1,AD=2.
=1,AD=2.
∵DF⊥AB,CB⊥AB,∴DF∥BC,∴∠ADF=∠ACB,∵∠A=∠A,∴△ADF∽△ACB,∴![]() ,设BC=x,则
,设BC=x,则![]() ,解得x=
,解得x=![]() ,∴BC=
,∴BC=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(操作发现】
在计算器上输入一个正数,不断地按“![]() ”键求算术平方根,运算结果越来越接近1或都等于1.
”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】
输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】
我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1,先在直线y=kx+b上确定点(x1,y1),再在直线y=x上确定纵坐标为y1的点(x2,y1),然后再x轴上确定对应的数x2,…,以此类推.
【解决问题】
研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
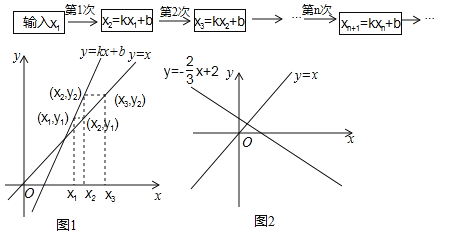
(1)若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若k>1,又得到什么结论?请说明理由;
(3)①若![]() ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息: 信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
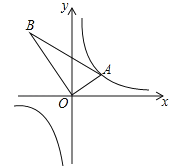
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数![]() 的图象上.若点B在反比例函数
的图象上.若点B在反比例函数![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
A.﹣4 B.4 C.﹣2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
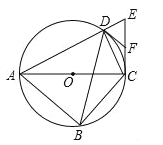
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com