
【题目】有一数值转换器,原理如图所示,如果开始输入![]() 的值为1,则第一次输出的结果是4,第二次输出的结果是5,……;那么2021次输出的结果是 _________ .
的值为1,则第一次输出的结果是4,第二次输出的结果是5,……;那么2021次输出的结果是 _________ .

【答案】10
【解析】
首先由数值转换器,发现第三次输出的结果是8为偶数,所以第四次输出的结果为7,第五次为10,第六次为8,第七次为7,…,可得出规律从第三次开始每三次一个循环,根据此规律求出第2021次输出的结果.
当输入1时,第一次输出1+3=4,
当输入4时,第二次输出![]() ×4+3=5,
×4+3=5,
当输入5时,第三次输出5+3=8,
当输入8时,第四次输出![]() ×8+3=7,
×8+3=7,
当输入7时,第五次输出7+3=10,
当输入10时,第六次输出![]() ×10+3=8,
×10+3=8,
当输入8时,第七次输出![]() ×8+3=7…
×8+3=7…
通过观察不难发现从第三次开始,输入三次一个循环.
∵(2021-2)÷3=673,
∴第2021次输出的结果为:10.
故答案为:10.


科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“已知底边及底边上的中线作等腰三角形”的尺规作图过程.

已知:如图 1,线段 a 和线段 b.
求作:△ABC,使得 AB = AC,BC = a,BC 边上的中线为 b.
作法:如图 ,
![]()
① 作射线 BM,并在射线 BM 上截取 BC = a;
② 作线段 BC 的垂直平分线 PQ,PQ 交 BC 于 D;
③ 以 D 为圆心,b 为半径作弧,交 PQ 于 A;
④ 连接 AB 和 AC.
则△ABC 为所求作的图形.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图 2 中的图形;
(2)完成下面的证明:
证明:由作图可知 BC = a,AD = b.
∵ PQ 为线段 BC 的垂直平分线,点 A 在 PQ 上,
∴ AB = AC( )(填依据).
又∵线段 BC 的垂直平分线 PQ 交 BC 于 D,
∴ BD=CD.( )(填依据).
∴ AD 为 BC 边上的中线,且 AD = b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
(1)请在图中标出景点C的位置;
(2)小明想从景点B开始游玩,途经景点A,最后到达景点C,求小明一家最短的行走路程(参考数据:![]() ≈6,结果保留整数).
≈6,结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个关于![]() 的代数式
的代数式![]() ,若存在一个系数为正数关于
,若存在一个系数为正数关于![]() 的单项式
的单项式![]() ,使
,使![]() 的结果是所有系数均为整数的整式,则称单项式
的结果是所有系数均为整数的整式,则称单项式![]() 为代数式
为代数式![]() 的“整系单项式” ,例如:
的“整系单项式” ,例如:
当![]() 时,由于
时,由于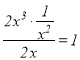 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于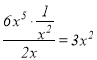 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于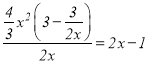 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于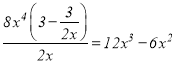 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
显然,当代数式![]() 存在整系单项式
存在整系单项式![]() 时,
时,![]() 有无数个,现把次数最低,系数最小的整系单项式
有无数个,现把次数最低,系数最小的整系单项式![]() 记为
记为![]() ,例如:
,例如:![]() .
.
阅读以上材料并解决下列问题:
⑴.判断:当![]() 时,
时,![]()
![]() 的整系单项式(填“是”或“不是”);
的整系单项式(填“是”或“不是”);
⑵.当![]() 时,
时,![]() = ;
= ;
⑶.解方程: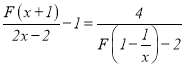 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信公司提供了![]() ,
,![]() 两种方案的移动通讯费用
两种方案的移动通讯费用![]() (元)与通话时间
(元)与通话时间![]() (分)之间的关系,则以下说法正确的是( )
(分)之间的关系,则以下说法正确的是( )
①若通话时间少于120分,则![]() 方案比
方案比![]() 方案便宜
方案便宜
②若通话时间超过200分,则![]() 方案比
方案比![]() 方案便宜
方案便宜
③通讯费用为60元,则![]() 方案比
方案比![]() 方案的通话时间多
方案的通话时间多
④当通话时间是170分钟/时,两种方案通讯费用相等
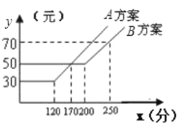
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
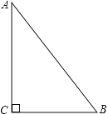
【题目】如图,△ABC中,∠C=90°,AC=4cm,BC=3cm,若动点P从点C开始,沿C→A→B→C的路径运动一周,且速度为每秒2cm,设运动时间为t秒,当t=_____时,点P与△ABC的某两个顶点构成等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com