
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() ,
,![]() 是
是![]() 上的三点,
上的三点,![]() ,
,![]() 点是
点是![]() 的中点,
的中点,![]() 点是
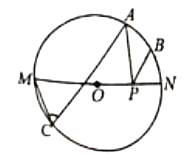
点是![]() 上一动点,若
上一动点,若![]() 的半径为1,则
的半径为1,则![]() 的最小值为( )
的最小值为( )
A.1B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
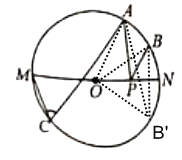
作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,根据轴对称确定最短路线问题可得PA+PB的最小值=AB′,根据在同圆或等圆中,同弧所对的圆心角等于圆周角的2倍求出∠AOM=120°,然后可得∠AON=60°,再求出∠BON=30°,根据对称性可得∠B′ON=∠BON=30°,然后易得∠AOB′=90°,从而判断出△AOB′是等腰直角三角形,再根据等腰直角三角形的性质可得AB′的长度.
解:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,则PA+PB的最小值=AB′,
∵∠ACM=60°,
∴∠AOM=120°,
∴∠AON=180°-∠AOM=60°,
∵点B为![]() 的中点,
的中点,
∴∠BON=![]() ∠AON=
∠AON=![]() ×60°=30°,
×60°=30°,
由对称性可得,∠B′ON=∠BON=30°,
∴∠AOB′=∠AON+∠B′ON=60°+30°=90°,
∴△AOB′是等腰直角三角形,
∴AB′=![]() OA=
OA=![]() ,即PA+PB的最小值为
,即PA+PB的最小值为![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·宁夏中考)如图,已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
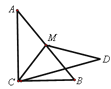
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,BC=m,D,E分别是AB,AC边的中点,点P为BC边上的一个动点,连接PD,PA,PE.设PC=x,图1中某条线段长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线可能是( )
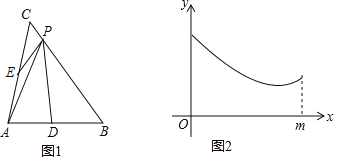
A.PBB.PEC.PAD.PD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com