练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

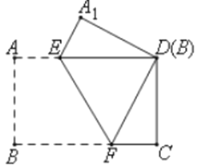
    【题目】把一张矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，折痕为EF,若BF=4, AE=2，则∠DEF的度数是_____。

    【答案】60°

    【解析】

    根据折叠的性质得到DF=BF=4，∠BFE=∠DFE，在Rt△DFC中，根据含30°的直角三角形三边的关系得到∠FDC=30°，则∠DFC=60°，所以有∠BFE=∠DFE=（180°-60°）÷2，然后利用两直线平行内错角相等得到∠DEF的度数．

    解：∵矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，折痕为EF，
    ∴DF=BF=4，∠BFE=∠DFE，
    在Rt△DFC中，FC=2，DF=4，
    ∴∠FDC=30°，
    ∴∠DFC=60°，
    ∴∠BFE=∠DFE=（180°-60°）÷2=60°，
    ∴∠DEF=∠BFE=60°．
    故答案为：60．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

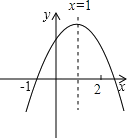
    【题目】已知二次函数y=ax2+bx+c的图象如图所示，对称轴为x=1，经过点（-1，0），有下列结论：①abc＜0；②a+c＞b；③3a+c=0；④a+b＞m（am+b）（其中m≠1）其中正确的结论有（　　）

    A. 1个

    B. 2个

    C. 3个

    D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料

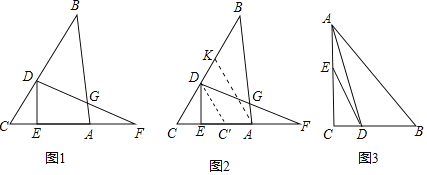
    小胖同学遇到这样一个问题：如图1，△ABC中，点D在BC上，点F是CA延长线上的点，连接DF交AB于G．过点D作DE⊥AC，垂足为E．若∠AGD＝2∠C，DF＝AB，求的值．

    小胖通过计算角度发现∠BGD＝2∠CDE，于是作出点C关于DE的对称点C′，使得∠CDC′＝∠BGD，进而得出∠C′DF＝∠B，接着截取BK＝DC，得出一组全等三角形．

    （1）请沿着小胖的思路继续完成此题的解答过程：

    （2）参考小胖的解题方法完成下面问题：

    如图3，在△ABC中，∠ACB＝2∠B，BD＝2CD，∠BAD＝∠CED，探索AE、CE、CD三条线段的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

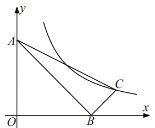
    【题目】如图，已知在平面直角坐标系中，Rt△ABC的顶点A、B的坐标分别是（0，3）、（3，0），∠ABC=90°AC=，则函数的图象经过点C，则的值为（ ）

    A.3B.4C.6D.9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据农业部提出“大力发展农村产业，实现乡村全面振兴”的方针，我市精确扶贫，指导某县大力发展大五星枇杷种植，去年、今年枇杷产量连续获得大丰收，该县枇杷销售采用线下销售和线上销售两种模式.

    （1）今年该县种植专业户大五星枇杷产量为4500千克，全部售出，其中线上销售量不超过线下销售的4倍，求该种植专业户线下销售量至少多少千克？

    （2）该种植专业户去年大五星枇杷线下销售均价为10元/千克，销售量为900千克，线上销售均价为8元/千克，销售量为1800千克，今年线下销售均价上涨，但销售量下降了，线上销售均价上涨了，销量与去年持平，今年大五星枇杷的销售总额比去年销售总额减少了，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)如图①,画一条平行于BC的直线，使其将△ABC分成两部分，且所分三角形与梯形面积比为1:3;

    (2)如图②，△ABC中AB=4，AC=3，BC=6，D是△ABC中AC边上的点，AD=2，过点D画一条直线l将△ABC分成两部分，l与△ABC另一边的交点为点P,使其所分的一个三角形与△ABC相似，并求出DP的长;

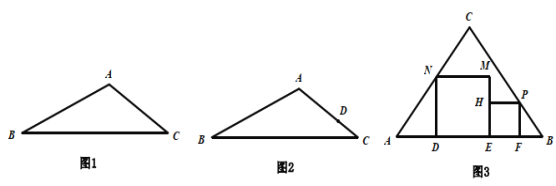
    (3)如图③所示，在等腰△ABC中，CA=CB=10，AB=12.在△ABC中放入正方形DEMN和正方形EFPH，使得DE.EF在边AB上，点P.N分别在边CB.CA上，若较大正方形的边长为a,请用含a的代数式表示较小正方形的边长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O为正方形ABCD对角线上一点，以点O为圆心，OA长为半径的

    ⊙ O与BC相切于点E．

    （1）求证：CD是⊙ O的切线；

    （2）若正方形ABCD的边长为10，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A，B，C，D是⊙O上的四个点．

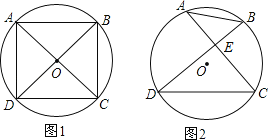
    （1）如图1，若∠ADC＝∠BCD＝90°，AD＝CD，求证：AC⊥BD；

    （2）如图2，若AC⊥BD．垂足为E，AB＝4，DC＝6，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是的直径，，，是上的三点，，点是的中点，点是上一动点，若的半径为1，则的最小值为（ ）

    A.1B.C.D.

    查看答案和解析>>

    同步练习册答案