
【题目】已知A,B,C,D是⊙O上的四个点.
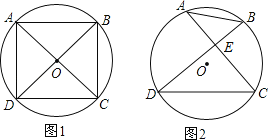
(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
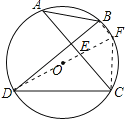
(2)如图2,若AC⊥BD.垂足为E,AB=4,DC=6,求⊙O的半径.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据题意不难证明四边形ABCD是正方形,从而得证;
(2)连接DO,延长交圆O于F,连接CF、BF.根据直径所对的圆周角是直角,得∠DCF=∠DBF=90°,则BF∥AC,根据平行弦所夹的弧相等,得![]() ,则CF=AB.根据勾股定理即可求解.
,则CF=AB.根据勾股定理即可求解.
(1)∵∠ADC=∠BCD=90°,
∴AC、BD是⊙O的直径,
∴∠DAB=∠ABC=90°,
∴四边形ABCD是矩形,
∵AD=CD,
∴四边形ABCD是正方形,
∴AC⊥BD;
(2)连接DO,延长交圆O于F,连接CF、BF.
∵DF是直径,
∴∠DCF=∠DBF=90°,
∴FB⊥DB,
又∵AC⊥BD,
∴BF∥AC,∠BDC+∠ACD=90°,
∵∠FCA+∠ACD=90°,
∴∠BDC=∠FCA=∠BAC,
∴四边形ACFB是等腰梯形,
∴CF=AB.
根据勾股定理,得CF2+DC2=AB2+DC2=DF2=52,
∴DF=2![]() ,
,
∴OD=![]() ,即⊙O的半径为
,即⊙O的半径为![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标x纵坐标y的对应值如下表
上部分点的横坐标x纵坐标y的对应值如下表
x |
|
|
| 0 | 1 | 2 |
|
y |
| 0 |
|
| 0 | 8 |
|
![]() 写出该抛物线的对称轴及当
写出该抛物线的对称轴及当![]() 时对应的函数值;
时对应的函数值;
![]() 求出抛物线
求出抛物线![]() 的解析式,并在平面直角坐标系中画出该抛物线的图象;
的解析式,并在平面直角坐标系中画出该抛物线的图象;
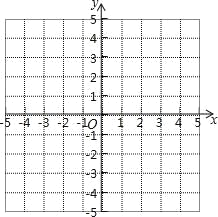
(3)结合图象回答:
①不等式![]() 的解集是___________________;
的解集是___________________;
②当![]() 时,y的取值范围是__________________.
时,y的取值范围是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,直线MN经过点A.
,直线MN经过点A.
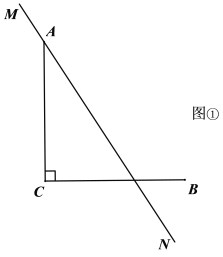
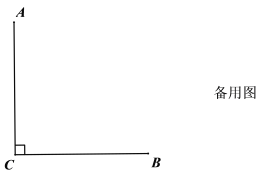
(1)作![]() ,垂足为D,连结CD,在图①中补全图形,猜想
,垂足为D,连结CD,在图①中补全图形,猜想![]()
![]() 的度数并证明;
的度数并证明;
(2)在直线MN绕点A旋转的过程中,当![]() ,
, ![]() 时,直接写出DC的长.
时,直接写出DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奇思参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题奇思都不会,不过奇思还有两个“求助”可以使用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果奇思两次“求助”都在第一道单选题中使用,求他通关的概率;
(2)如果奇思每道单选题各使用一次“求助",请用列表法或画树状图的方法求他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
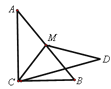
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com