
【题目】阅读下面材料
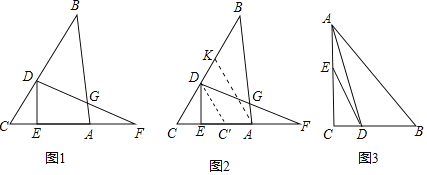
小胖同学遇到这样一个问题:如图1,△ABC中,点D在BC上,点F是CA延长线上的点,连接DF交AB于G.过点D作DE⊥AC,垂足为E.若∠AGD=2∠C,DF=AB,求![]() 的值.
的值.
小胖通过计算角度发现∠BGD=2∠CDE,于是作出点C关于DE的对称点C′,使得∠CDC′=∠BGD,进而得出∠C′DF=∠B,接着截取BK=DC,得出一组全等三角形.
(1)请沿着小胖的思路继续完成此题的解答过程:
(2)参考小胖的解题方法完成下面问题:
如图3,在△ABC中,∠ACB=2∠B,BD=2CD,∠BAD=∠CED,探索AE、CE、CD三条线段的数量关系.
【答案】(1)![]() ;(2)AE=CE﹣CD.
;(2)AE=CE﹣CD.
【解析】
(1)根据SAS可证明△ABK≌△FDC',得出AK=FC',∠AKB=∠FC'D,证明CE=C′E,则可求出![]() ;
;
(2)作∠BDF=∠B交AB于F点,延长BC到G点,使得CG=CA,证明△CED∽△FAD,得出比例线段![]() ,设CD=x,BD=2x,CE=y,可得出DG=2y,则CG=AC=DG=2y-x,可得出AE=y-x=CE-CD.
,设CD=x,BD=2x,CE=y,可得出DG=2y,则CG=AC=DG=2y-x,可得出AE=y-x=CE-CD.
(1)∵BK=CD=C′D,∠C′DF=∠B,DF=AB,
∴△ABK≌△FDC'(SAS),
∴AK=FC',∠AKB=∠FC'D,
∴∠C=∠AKC,
∴AK=AC=FC′,
∵DE⊥CC',且DC=DC',
∴CE=C′E,
∴AF=2CE,
∴![]() ;
;
(2)AE=CE﹣CD.
如图,作∠BDF=∠B交AB于F点,延长BC到G点,使得CG=CA,
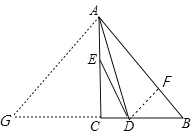
∴DF=FB,
∴∠FDB=∠B,
∴∠G=∠CAG=∠B=∠FDB,
∴DF∥AG,∠ECD=2∠B,
∴∠AFD=∠ECD,∠CED=∠FAD,
∴△CED∽△FAD,
∴![]() ,
,
设CD=x,BD=2x,CE=y,
∴![]() ,
,
∴![]() ,
,
∴DG=2y,
∴CG=AC=DG﹣CD=2y﹣x,
∴AE=AC﹣CE=y﹣x=CE﹣CD.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,以BC为直径的半圆交AB于点D,O是该半圆所在圆的圆心,E为线段AC上一点,且ED=EA.
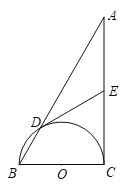
(1)求证:ED是⊙O的切线;
(2)若![]() ,∠A=30°,求⊙O的半径.
,∠A=30°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
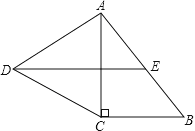
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴交于A(﹣2,0)、B(4,0)两点,且函数经过点(3,10).
(1)求二次函数的解析式;
(2)设这个二次函数的顶点为P,求△ABP的面积;
(3)当x为何值时,y≤0.(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,A(0,8)、B(6,0) .动点P从A点出发,沿y轴负半轴方向运动,速度每秒2个单位长度,动点Q从B点出发,沿BA方向向A点运动,速度每秒1个单位长度.两点同时出发,Q点到达A点时,两点同时停止运动,运动时间为t秒.
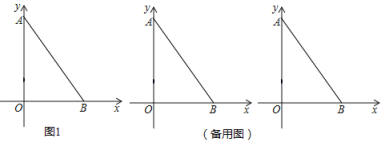
(1)当△APQ面积为12,求t的值.
(2)当△APQ的外心(三角形的外心是三角形三边垂直平分线的交点)在△APQ的边上时,求t值.
(3)若Q点在直线AB上运动,过Q点作QH⊥x轴,垂足为H,当△QBH与△ABO的相似比为1:2时,直接写出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
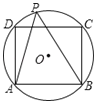
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com