
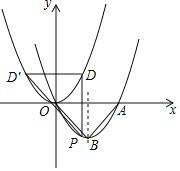
【题目】如图,在平面直角坐标系中有抛物线y=a(x﹣2)2﹣2和y=a(x﹣h)2,抛物线y=a(x﹣2)2﹣2经过原点,与x轴正半轴交于点A,与其对称轴交于点B;点P是抛物线y=a(x﹣2)2﹣2上一动点,且点P在x轴下方,过点P作x轴的垂线交抛物线y=a(x﹣h)2于点D,过点D作PD的垂线交抛物线y=a(x﹣h)2于点D′(不与点D重合),连接PD′,设点P的横坐标为m:
(1)①直接写出a的值;
②直接写出抛物线y=a(x﹣2)2﹣2的函数表达式的一般式;
(2)当抛物线y=a(x﹣h)2经过原点时,设△PDD′与△OAB重叠部分图形周长为L:
①求![]() 的值;
的值;
②直接写出L与m之间的函数关系式;
(3)当h为何值时,存在点P,使以点O、A、D、D′为顶点的四边形是菱形?直接写出h的值.
【答案】(1)①![]() ;②y=
;②y=![]() ﹣2x;
﹣2x;
(2)①1;
②L=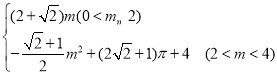 ;
;
(3)h=±![]() .
.
【解析】
(1)①将x=0,y=0代入y=a(x﹣2)2﹣2中计算即可;②y=![]() ﹣2x;
﹣2x;
(2)将(0,0)代入y=a(x﹣h)2中,可求得a=![]() ,y=
,y=![]() x2,待定系数法求OB、AB的解析式,由点P的横坐标为m,即可表示出相应线段求解;
x2,待定系数法求OB、AB的解析式,由点P的横坐标为m,即可表示出相应线段求解;
(3)以点O、A、D、D′为顶点的四边形是菱形,DD′=OA,可知点D的纵坐标为2,再由AD=OA=4即可求出h的值.
解:(1)①将x=0,y=0代入y=a(x﹣2)2﹣2中,
得:0=a(0﹣2)2﹣2,
解得:a=![]() ;
;
②y=![]() ﹣2x;.
﹣2x;.
(2)∵抛物线y=a(x﹣h)2经过原点,a=![]() ;
;
∴y=![]() x2,
x2,
∴A(4,0),B(2,﹣2),
易得:直线OB解析式为:y=﹣x,直线AB解析式为:y=x﹣4
如图1,

![]() ,
,
①![]()
![]()
②如图1,当0<m≤2时,L=OE+EF+OF=![]() ,
,
当2<m<4时,如图2,设PD′交x轴于G,交AB于H,PD交x轴于E,交AB于F,

则![]() ,
,
![]() ,
,
![]()
∵DD′∥EG
![]() ,即:EGPD=PEDD′,得:EG(2m)=(2m﹣
,即:EGPD=PEDD′,得:EG(2m)=(2m﹣![]() m2)2m
m2)2m
∴EG=2m﹣![]() m2,EF=4﹣m
m2,EF=4﹣m
∴L=EG+EF+FH+GH=EG+EF+PG
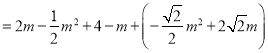
![]()
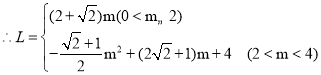 ;
;
(3)如图3,

∵OADD′为菱形
∴AD=AO=DD′=4,
∴PD=2,
![]()
![]()


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面![]() 的坡度为
的坡度为![]() ,文化墙
,文化墙![]() 在天桥底部正前方8米处(
在天桥底部正前方8米处(![]() 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为
的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为![]() .(参考数据:
.(参考数据:![]() ,
,![]() )
)
(1)若新坡面坡角为![]() ,求坡角
,求坡角![]() 度数;
度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙![]() 是否需要拆除?请说明理由.
是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
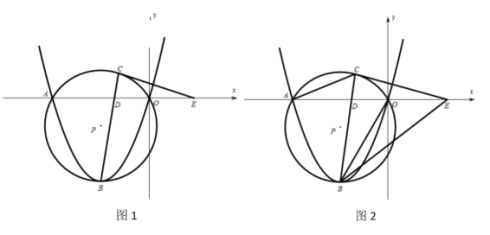
【题目】如图,抛物线![]() (a为常数,a>0)与x轴交于O,A两点,点B为抛物线的顶点,点D的坐标为(t,0)(﹣3<t<0),连接BD并延长与过O,A,B三点的⊙P相交于点C.
(a为常数,a>0)与x轴交于O,A两点,点B为抛物线的顶点,点D的坐标为(t,0)(﹣3<t<0),连接BD并延长与过O,A,B三点的⊙P相交于点C.
(1)求点A的坐标;
(2)过点C作⊙P的切线CE交x轴于点E.①如图1,求证:CE=DE;②如图2,连接AC,BE,BO,当![]() ,∠CAE=∠OBE时,求
,∠CAE=∠OBE时,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
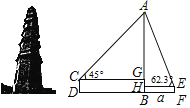
【题目】慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮与塔底中心的距离BD;(用含a的式子表示)
(2)若小亮与小琴相距52米,求慈氏塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的一带一路经济发展战略,树立品牌意识,我市质检部分别对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图:
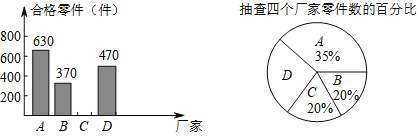
(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 度;
(2)抽查C厂家的合格率零件为 件,并将图1补充完整;
(3)通过计算说明A、C两厂家谁的合格率更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解答下列各题:
(1)如图①,求作一点![]() ,使点
,使点![]() 到
到![]() 的两边的距离相等,且在
的两边的距离相等,且在![]() 的边
的边![]() 上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明);
上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明);
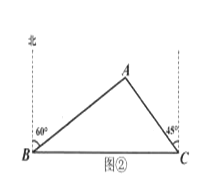
(2)如图②,![]() 表示两个港口,港口
表示两个港口,港口![]() 在港口
在港口![]() 的正东方向上.海上有一小岛
的正东方向上.海上有一小岛![]() 在港口
在港口![]() 的北偏东
的北偏东![]() 方向上,且在港口
方向上,且在港口![]() 的北偏西
的北偏西![]() 方向上.测得
方向上.测得![]() 海里,求小岛
海里,求小岛![]() 与港口
与港口![]() 之间的距离.(结果可保留根号)
之间的距离.(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
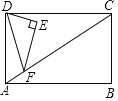
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3(a≠0),且a+b=3.
(1)若其图象经过点(﹣3,0),求此二次函数的表达式.
(2)若(m,n)为(1)中二次函数图象在第三象限内的点,请分别求m,n的取值范围.
(3)点P(x1,y1),Q(x2,y2)是函数图象上两个点,满足x1+x2=2且x1<x2,试比较y1和y2的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com