Question

【题目】操作：

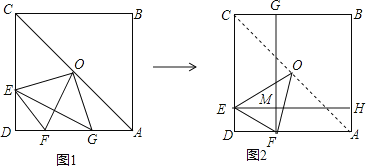
如图1，正方形ABCD中，AB=a，点E是CD边上一个动点，在AD上截取AG=DE，连接EG，过正方形的中线O作OF⊥EG交AD边于F，连接OE、OG、EF、AC．

探究：

在点E的运动过程中：

（1）猜想线段OE与OG的数量关系？并证明你的结论；

（2）∠EOF的度数会发生变化吗？若不会，求出其度数，若会，请说明理由．

应用：

（3）当a=6时，试求出△DEF的周长，并写出DE的取值范围；

（4）当a的值不确定时：

①若=时，试求的值；

②在图1中，过点E作EH⊥AB于H，过点F作FG⊥CB于G，EH与FG相交于点M；并将图1简化得到图2，记矩形MHBG的面积为S，试用含a的代数式表示出S的值，并说明理由．

Answer 1

【答案】（1）OE=OG，理由参见解析；（2）不会发生变化，∠EOF=45°；（3）6，（0＜DE＜3）；（4）①，②S=a2，理由参见解析.

【解析】试题分析：（1）连接OD,由正方形的性质和已知条件得到△AOG≌△DOE即可；（2）由△AOG≌△DOE得到结论，再结合同角或等角的余角相等求出∠EOF；（3）判断出OF垂直平分EG，计算出周长=DE+EF+DF=AG+FG+DF=AD=AB=6即可；（4）①先判断出△AOF∽△CEO，得出S△AOF:S△CEO=AF:CE，进而求出．②由△AOF∽△CEO得出对应线段成比例，可导出AF×CE=OA×OC，因为S=AF×CE，所以可求出S=OA×OC=a2.

试题解析：（1）OE=OG，理由：如图1，

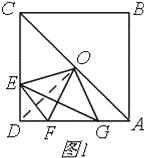
连接OD，在正方形ABCD中，∵点O是正方形中心，∴OA=OD，∠OAD=∠ODC=45°，

∵AG=DE，∴△AOG≌△DOE，∴OE=OG；（2）∠EOF的度数不会发生变化，理由：由（1）可知，△AOG≌△DOE，∴∠DOE=∠AOG，∵∠AOG+∠DOG=90°，∴∠DOE+∠DOG=90°，∴∠DOE=∠AOG，∵∠EOG=90°，∵OE=OG，OF⊥EG，∴∠EOF=45°，∴∠EOF恒为定值；（3）由（2）可知，OE=OG，OF⊥EG，∴OF垂直平分EG，∴△DEF的周长为DE+EF+DF=AG+FG+DF=AD，∵AB=a=6，∴△DEF的周长为AD=AB=a=6，（0＜DE＜3）；（4）①如图2，

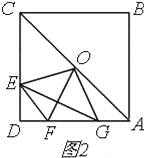
∵∠EOF=45°，∴∠COE+AOF=135°∵∠OAF=45°，∴∠AFO+∠AOF=135°，∴∠COE=∠AFO，∴△AOF∽△CEO，∴S△AOF:S△CEO=(OF:OE)2，∵O到AF与CE的距离相等，∴S△AOF:S△CEO=AF:CE，

∴（）2=，∵＞0，∴=，②猜想：S=a2，理由：如图3，

由（1）可知，△AOF∽△CEO，∴，∴AF×CE=OA×OC，∵EH⊥AB，FG⊥CB，∠B=90°，∴S=AF×CE，∴S=OA×OC=×=a2．