
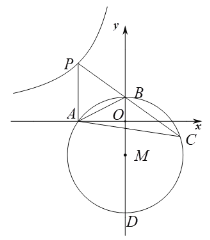
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 上,
上,![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() 、
、![]() 的长是方程
的长是方程![]() 的两个实数根,且
的两个实数根,且![]() ,点
,点![]() 是线段
是线段![]() 延长线上的一个动点,
延长线上的一个动点,![]() 的外接圆
的外接圆![]() 与
与![]() 轴的另一个交点是
轴的另一个交点是![]() .
.
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)求反比例函数的解析式;
(3)连接![]() 求
求![]() 的值.
的值.
【答案】(1)点A坐标为(-6,0),点B坐标为(0,2);(2)反比例函数解析式为:![]() ;(3)
;(3)![]() .
.
【解析】
(1)先解一元二次方程求出线段长,再转化为坐标即可;
(2)设出点P坐标,根据PA=PB建立方程求解即可;
(3)连接AM,设半径为r,在Rt△AOM中利用勾股定理求出半径长,再过点P作PH⊥y轴,根据线段之间的关系得到HM的长度,在Rt△PMH中即可求出结果.
解:(1)![]() ,解得:
,解得:![]() 或
或![]() ,
,
∵OA,OB的长是方程![]() 的两个实数根,且OA>OB,
的两个实数根,且OA>OB,
∴OA=6,OB=2,
∴点A坐标为(-6,0),点B坐标为(0,2);
(2)设点![]() ,由
,由![]() 知
知![]() ,
,
∴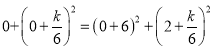 ,
,
解得:![]() ,
,
∴点P(-6,10),反比例函数解析式为:![]() ;
;
(3)连接AM,设半径为r,则OM=r-2,
∵在![]() 中,
中,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴BM=AM=10,
过点P作PH⊥y轴,则OH =10,PH=6,
∴HB=OH-OB=8,
∴HM=HB+BM=18,
∴在![]() 中,
中,![]() .
.


科目:初中数学 来源: 题型:
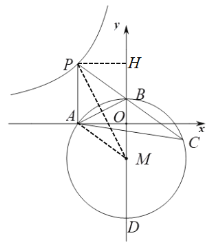
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
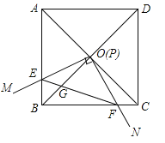
【题目】已知:如图,四边形ABCD是边长为1的正方形,对角线AC、BD相交于点O.过点O作一直角∠MON,直角边OM、ON分别与OA、OB重合,然后逆时针旋转∠MON,旋转角为θ(0°<θ<90°),OM、ON分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是________(填序号).
①![]() ;②S四边形OEBF:S正方形ABCD=1:2;③
;②S四边形OEBF:S正方形ABCD=1:2;③![]() ;④OGBD=AE2+CF2;⑤在旋转过程中,当△BEF与△COF的面积之和最大时,
;④OGBD=AE2+CF2;⑤在旋转过程中,当△BEF与△COF的面积之和最大时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
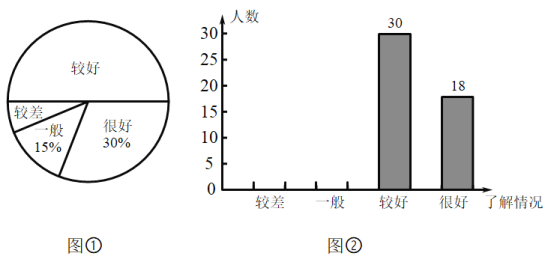
【题目】“安全教育,警钟长鸣”,为此,某校随机抽取了九年级(1)班的学生对安全知识的了解情况进行了一次调查统计.图①和图②是通过数据收集后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)九年级(1)班共有多少名学生;
(2)补全图②;
(3)在扇形统计图中,对安全知识的了解情况为“较差”部分所对应的圆心角的度数是多少;
(4)若全校有1500名学生,估计对安全知识的了解情况为“较差”、“一般”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把分子为1的分数叫做单位分数,如:![]() ,
,![]() ,
,![]() ,任何一个单位分数都可以拆分成两个不同的单位分数的和,如“
,任何一个单位分数都可以拆分成两个不同的单位分数的和,如“![]() =
=![]() +
+![]() ”,“
”,“![]() =
=![]() +
+![]() ”……
”……
(1)根据对上述式子的观察,你会发现.![]() =
=![]() ·请将问题中的空格补充完整.
·请将问题中的空格补充完整.
(2)进一步思考,单位分数![]() (n是不小于2的正整数),请写出■和●所表示的代数式,并对你的结论进行验证.
(n是不小于2的正整数),请写出■和●所表示的代数式,并对你的结论进行验证.
(3)请用(2)中你找出的规律解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
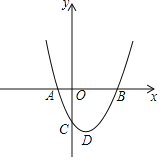
【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,﹣3),顶点D的坐标为(1,﹣4).
(1)求抛物线的解析式.
(2)在y轴上找一点E,使得△EAC为等腰三角形,请直接写出点E的坐标.
(3)点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸在176~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下.
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据

分析数据
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
(1)求![]() ,
,![]() 的值;
的值;
(2)计算甲车间样品的合格率;
(3)估计乙车间生产的1000个该款新产品中合格产品有多少个;
(4)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )
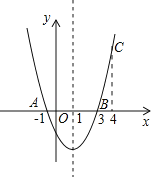
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com