
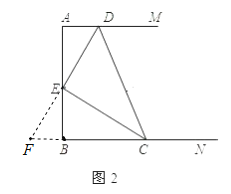
ЁОЬтФПЁПвбжЊЃКШчЭМЃЈ1ЃЉЃЌЩфЯпAMЁЮЩфЯпBNЃЌABЪЧЫќУЧЕФЙЋДЙЯпЃЌЕуDЁЂCЗжБ№дкAMЁЂBNЩЯдЫЖЏЃЈЕуDгыЕуAВЛжиКЯЁЂЕуCгыЕуBВЛжиКЯЃЉЃЌEЪЧABБпЩЯЕФЖЏЕуЃЈЕуEгыAЁЂBВЛжиКЯЃЉЃЌдкдЫЖЏЙ§ГЬжаЪМжеБЃГжDEЁЭECЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁзЁїBECЃЛ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌЕБЕуEЮЊABБпЕФжаЕуЪБЃЌЧѓжЄЃКAD+BC=CDЃЛ
ЃЈ3ЃЉЕБ AD+DE=AB=![]() ЪБЃЎЩшAE=mЃЌЧыЬНОПЃКЁїBECЕФжмГЄЪЧЗёгыmжЕгаЙиЃПШєгаЙиЃЌЧыгУКЌгаmЕФДњЪ§ЪНБэЪОЁїBECЕФжмГЄЃЛШєЮоЙиЃЌЧыЫЕУїРэгЩЃЎ
ЪБЃЎЩшAE=mЃЌЧыЬНОПЃКЁїBECЕФжмГЄЪЧЗёгыmжЕгаЙиЃПШєгаЙиЃЌЧыгУКЌгаmЕФДњЪ§ЪНБэЪОЁїBECЕФжмГЄЃЛШєЮоЙиЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉ![]() ЕФжмГЄгыmжЕЮоЙиЃЌРэгЩЯъМћНтЮіЃЎ
ЕФжмГЄгыmжЕЮоЙиЃЌРэгЩЯъМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩжБНЧЬнаЮABCDжаЁЯAЮЊжБНЧЃЌЕУЕНШ§НЧаЮADEЮЊжБНЧШ§НЧаЮЃЌПЩЕУГіСНШёНЧЛЅгрЃЌдйгЩDEгыECДЙжБЃЌРћгУДЙжБЕФЖЈвхЕУЕНЁЯDECЮЊжБНЧЃЌРћгУЦННЧЕФЖЈвхЭЦГівЛЖдНЧЛЅгрЃЌРћгУЭЌНЧЕФгрНЧЯрЕШПЩЕУГівЛЖдНЧЯрЕШЃЌдйгЩвЛЖджБНЧЯрЕШЃЌРћгУСНЖдЖдгІНЧЯрЕШЕФСНШ§НЧаЮЯрЫЦПЩЕУжЄЃЛ
ЃЈ2ЃЉбгГЄDEЁЂCBНЛгкFЃЌжЄУїЁїADEЁеЁїBFEЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНDE=FEЃЌAD=BFгЩCEЁЭDEЃЌЕУЕНжБЯпCEЪЧЯпЖЮDFЕФДЙжБЦНЗжЯпЃЌгЩЯпЖЮДЙжБЦНЗжЯпЕФаджЪЕУDC=FCЃЎМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉЁїBECЕФжмГЄгыmЕФжЕЮоЙиЃЌРэгЩЮЊЃКЩшAD=xЃЌгЩAD+DE=aЃЌБэЪОГіDEЃЎдкжБНЧШ§НЧаЮADEжаЃЌРћгУЙДЙЩЖЈРэСаГіЙиЯЕЪНЃЌећРэКѓМЧзїЂйЃЌгЩABЉAE=EBЃЌБэЪОГіBEЃЌИљОнЃЈ1ЃЉЕУЕНЃКЁїADEЁзЁїBECЃЌгЩЯрЫЦЕУБШР§ЃЌНЋИїздБэЪОГіЕФЪНзгДњШыЃЌБэЪОГіBCгыECЃЌгЩEB+EC+BCБэЪОГіШ§НЧаЮEBCЕФжмГЄЃЌЬсШЁaЉmКѓЃЌЭЈЗжВЂРћгУЭЌЗжФИЗжЪНЕФМгЗЈЗЈдђМЦЫуЃЌдйРћгУЦНЗНВюЙЋЪНЛЏМђКѓЃЌМЧзїЂкЃЌНЋЂйДњШыЂкЃЌдМЗжКѓЕУЕНвЛИіВЛКЌmЕФЪНзгЃЌМДжмГЄгыmЮоЙиЃЎ
ЃЈ1ЃЉЁпжБНЧЬнаЮABCDжаЃЌЁЯA=90ЁуЃЌ
ЁрЁЯADE+ЁЯAED=90ЁуЃЌ
гжЁпDEЁЭCEЃЌ
ЁрЁЯDEC=90ЁуЃЌ
ЁрЁЯAED+ЁЯBEC=90ЁуЃЌ
ЁрЁЯADE=ЁЯBECЃЌ
гжЁпЁЯA=ЁЯB=90ЁуЃЌ
ЁрЁїADEЁзЁїBECЃЛ
ЃЈ2ЃЉбгГЄDEЁЂCBНЛгкFЃЌШчЭМ2ЫљЪОЃЎ
ЁпADЁЮBCЃЌ
ЁрЁЯA=ЁЯEBFЃЌЁЯADE=ЁЯFЃЎ
ЁпEЪЧABЕФжаЕуЃЌ
ЁрAE=BEЃЎ
дкЁїADEКЭЁїBFEжаЃЌЁпЁЯA=ЁЯEBFЃЌЁЯADE=ЁЯFЃЌAE=BEЃЌ
ЁрЁїADEЁеЁїBFEЃЌ
ЁрDE=FEЃЌAD=BFЃЎ
ЁпCEЁЭDEЃЌ
ЁржБЯпCEЪЧЯпЖЮDFЕФДЙжБЦНЗжЯпЃЌ
ЁрDC=FCЃЎ
ЁпFC=BC+BF=BC+ADЃЌ
ЁрAD+BC=CDЃЎ
ЃЈ3ЃЉЁїBECЕФжмГЄгыmЕФжЕЮоЙиЃЌРэгЩЮЊЃК
ЩшAD=xЃЌгЩAD+DE=AB=aЃЌЕУЃКDE=aЉxЃЎ
дкRtЁїAEDжаЃЌИљОнЙДЙЩЖЈРэЕУЃКAD2+AE2=DE2ЃЌМДx2+m2=(aЉx)2ЃЌ
ећРэЕУЃКa2Љm2=2axЃЌЁЂй
дкЁїEBCжаЃЌгЩAE=mЃЌAB=aЃЌЕУЃКBE=ABЉAE=aЉmЃЎ
ЁпгЩЃЈ1ЃЉжЊЁїADEЁзЁїBECЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУЃКBC![]() ЃЌEC
ЃЌEC![]() ЃЌ
ЃЌ
ЁрЁїBECЕФжмГЄ=BE+BC+EC=(aЉm)![]()
=(aЉm)(1![]() )=(aЉm)
)=(aЉm)![]()
![]() ЃЌЁЂк
ЃЌЁЂк
АбЂйДњШыЂкЕУЃКЁїBECЕФжмГЄ=BE+BC+EC![]() 2aЃЌ
2aЃЌ
дђЁїBECЕФжмГЄгыmЮоЙиЃЎ


 жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЬНОПЃК
ШчЭМЃЌНЋХзЮяЯп![]() ЯђгвЦНвЦ
ЯђгвЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйЯђЯТЦНвЦ
ИіЕЅЮЛГЄЖШЃЌдйЯђЯТЦНвЦ![]() ИіЕЅЮЛГЄЖШКѓЃЌЕУЕНЕФХзЮяЯп
ИіЕЅЮЛГЄЖШКѓЃЌЕУЕНЕФХзЮяЯп![]() ЃЌЦНвЦКѓЕФХзЮяЯп
ЃЌЦНвЦКѓЕФХзЮяЯп![]() гы
гы![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() ,
,![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() .ХзЮяЯп
.ХзЮяЯп![]() ЕФЖдГЦжс
ЕФЖдГЦжс![]() гыХзЮяЯп
гыХзЮяЯп![]() НЛгкЕу
НЛгкЕу![]() .
.

ЃЈ1ЃЉЧыФужБНгаДГіХзЮяЯп![]() ЕФНтЮіЪНЃЛЃЈаДГіЖЅЕуЪНМДПЩЃЉ
ЕФНтЮіЪНЃЛЃЈаДГіЖЅЕуЪНМДПЩЃЉ
ЃЈ2ЃЉЧѓГі![]() ,
,![]() ,
,![]() Ш§ЕуЕФзјБъЃЛ
Ш§ЕуЕФзјБъЃЛ
ЃЈ3ЃЉдк![]() жсЩЯДцдквЛЕу
жсЩЯДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжЕзюаЁЃЌЧѓЕу
ЕФжЕзюаЁЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЪЕМљ
дкЪ§бЇЛюЖЏПЮЩЯЃЌРЯЪІГіЪОСЫетбљвЛИіЮЪЬтЃКШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() БпЩЯЕФШЮвтвЛЕуЃЎНЋ
БпЩЯЕФШЮвтвЛЕуЃЎНЋ![]() биЙ§Еу
биЙ§Еу![]() ЕФжБЯпелЕўЃЌЪЙЕу
ЕФжБЯпелЕўЃЌЪЙЕу![]() ТфдкаББп
ТфдкаББп![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ДІЃЎЮЪЪЧЗёДцдк
ДІЃЎЮЪЪЧЗёДцдк![]() ЪЧжБНЧШ§НЧаЮЃПШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛШєДцдкЃЌЧѓГіДЫЪБ
ЪЧжБНЧШ§НЧаЮЃПШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛШєДцдкЃЌЧѓГіДЫЪБ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ

ЬНОПеЙЪОЃКЧкЗмаЁзщКмПьевЕНСЫЕу![]() ЁЂ
ЁЂ![]() ЕФЮЛжУЃЎ
ЕФЮЛжУЃЎ
ШчЭМ2ЃЌзї![]() ЕФНЧЦНЗжЯпНЛ
ЕФНЧЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() би
би![]() ЫљдкЕФжБЯпелЕўЃЌЕу
ЫљдкЕФжБЯпелЕўЃЌЕу![]() ЧЁКУдк
ЧЁКУдк![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЫљвд
ЃЌЫљвд![]() ЪЧжБНЧШ§НЧаЮЃЎ
ЪЧжБНЧШ§НЧаЮЃЎ
ЮЪЬтНтОі:
ЃЈ1ЃЉАДЧкЗмаЁзщЕФетжжелЕўЗНЪНЃЌ![]() ЕФГЄЖШЮЊ ЃЎ
ЕФГЄЖШЮЊ ЃЎ
ЃЈ2/span>ЃЉДДаТаЁзщПДЭъЧкЗмаЁзщЕФелЕўЗНЗЈКѓЃЌЗЂЯжЛЙгаСэвЛжжелЕўЗНЗЈЃЌЧыдкЭМ3жаЛГіРДЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧѓГі![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=aЃЈx-1ЃЉ2+kгыxжсСНИіНЛЕуМфЕФОрРыЮЊ2ЃЌНЋХзЮяЯпy=aЃЈx-1ЃЉ2+kЯђЩЯЦНвЦnИіЕЅЮЛЃЌЦНвЦКѓЕФХзЮяЯпОЙ§Еу(mЃЌn)ЃЌдђmЕФжЕЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбСНЬѕПэЖШЖМЮЊ![]() ЕФжНЬѕНЛВцжиЕўЗХдквЛЦ№ЃЌЧвЫќУЧЕФНЛНЧЮЊ
ЕФжНЬѕНЛВцжиЕўЗХдквЛЦ№ЃЌЧвЫќУЧЕФНЛНЧЮЊ![]() ЃЌдђЫќУЧжиЕўВПЗжЃЈЭМжавѕгАВПЗжЃЉЕФУцЛ§ЮЊЃЈ ЃЉЃЎ
ЃЌдђЫќУЧжиЕўВПЗжЃЈЭМжавѕгАВПЗжЃЉЕФУцЛ§ЮЊЃЈ ЃЉЃЎ
A.![]() B.
B.![]()
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§гыxжсЃЌyжсЕФНЛЕуЗжБ№ЪЧAЃЈЉ4ЃЌ0ЃЉЃЌBЃЈ0ЃЌ2ЃЉЃЎгыЗДБШР§КЏЪ§ЕФЭМЯѓНЛгкЕуQЃЌЗДБШР§КЏЪ§ЭМЯѓЩЯгавЛЕуPТњзуЃКЂйPAЁЭxжсЃЛЂкPOЃН![]() ЃЈOЮЊзјБъдЕуЃЉЃЌдђЫФБпаЮPAQOЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
ЃЈOЮЊзјБъдЕуЃЉЃЌдђЫФБпаЮPAQOЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ

A.7B.10C.4+2![]() D.4Љ2
D.4Љ2![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМ1ЪЧФГдЁЪвЛЈШїЪЕОАЭМЃЌЭМ2ЪЧИУЛЈШїЕФВрУцЪОвтЭМЃЎвбжЊЛюЖЏЕїНкЕуBПЩвдЩЯЯТЕїећИпЖШЃЌРыЕиУцCDЕФОрРыBCЃН160cmЃЎЩшЛЈШїБлгыЧНУцЕФМаНЧЮЊІСЃЌПЩвдХЄЖЏЛЈШїБлЕїећНЧЖШЃЌЧвЛЈШїБлГЄABЃН30cmЃЎМйЩшЫЎжљAEДЙжБABжБЯпХчЩфЃЌаЁЛЊдкРыЧНУцОрРыCDЃН120cmДІСмдЁЃЎ

ЃЈ1ЃЉЕБІСЃН30ЁуЪБЃЌЫЎжље§КУТфдкаЁЛЊЕФЭЗЖЅЩЯЃЌЧѓаЁЛЊЕФЩэИпDEЃЎ
ЃЈ2ЃЉШчЙћаЁЛЊвЊЯДНХЃЌашвЊЕїећЫЎжљAEЃЌЪЙЕуEгыЕуDжиКЯЃЌЕїећЕФЗНЪНгаСНжжЃК
ЂйЦфЫћЬѕМўВЛБфЃЌжЛвЊАбЛюЖЏЕїНкЕуBЯђЯТвЦЖЏМДПЩЃЌвЦЖЏЕФОрРыBFгыаЁЛЊЕФЩэИпDEгаЪВУДЪ§СПЙиЯЕЃПжБНгаДГіФуЕФНсТлЃЛ
ЂкЛюЖЏЕїНкЕуBВЛЖЏЃЌжЛвЊЕїећІСЕФДѓаЁЃЌдкЭМ3жаЃЌЪдЧѓІСЕФЖШЪ§ЃЎ
ЃЈВЮПМЪ§ОнЃК![]() Ёж1.73ЃЌsin8.6ЁуЁж0.15ЃЌsin36.9ЁуЁж0.60ЃЌtan36.9ЁуЁж0.75ЃЉ
Ёж1.73ЃЌsin8.6ЁуЁж0.15ЃЌsin36.9ЁуЁж0.60ЃЌtan36.9ЁуЁж0.75ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓгыxжсЗжБ№НЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЎШєtanЁЯABC=3ЃЌвЛдЊЖўДЮЗНГЬax2+bx+c=0ЕФСНИљЮЊЉ8ЁЂ2ЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБЯпlШЦЕуAвдABЮЊЦ№ЪМЮЛжУЫГЪБеыа§зЊЕНACЮЛжУЭЃжЙЃЌlгыЯпЖЮBCНЛгкЕуDЃЌPЪЧADЕФжаЕуЃЎ
ЂйЧѓЕуPЕФдЫЖЏТЗГЬЃЛ
ЂкШчЭМ2ЃЌЙ§ЕуDзїDEДЙжБxжсгкЕуEЃЌзїDFЁЭACЫљдкжБЯпгкЕуFЃЌСЌНсPEЁЂPFЃЌдкlдЫЖЏЙ§ГЬжаЃЌЁЯEPFЕФДѓаЁЪЧЗёИФБфЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНсEFЃЌЧѓЁїPEFжмГЄЕФзюаЁжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЖдФўВЈЪаЯрЙиЕФЪаГЁЮяМлЕїбаЃЌФГХњЗЂЪаГЁФкМзжжЫЎЙћЕФЯњЪлРћШѓy1ЃЈЧЇдЊЃЉгыНјЛѕСПxЃЈЖжЃЉНќЫЦТњзуКЏЪ§ЙиЯЕ![]() ЃЌввжжЫЎЙћЕФЯњЪлРћШѓ
ЃЌввжжЫЎЙћЕФЯњЪлРћШѓ![]() ЃЈЧЇдЊЃЉгыНјЛѕСПxЃЈЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕНќЫЦгкЖўДЮКЏЪ§ЃЌКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
ЃЈЧЇдЊЃЉгыНјЛѕСПxЃЈЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕНќЫЦгкЖўДЮКЏЪ§ЃЌКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ

ЃЈ1ЃЉЧѓГі![]() гыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
гыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШчЙћИУЪаГЁзМБИНјМзЁЂввСНжжЫЎЙћЙВ8ЖжЃЌЩшввЫЎЙћЕФНјЛѕСПЮЊtЖжЃЌаДГіетСНжжЫЎЙћЫљЛёЕУЕФЯњЪлРћШѓжЎКЭWЃЈЧЇдЊЃЉгыtЃЈЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіетСНжжЫЎЙћИїНјЖрЩйЖжЪБЃЌЛёЕУЕФЯњЪлРћШѓжЎКЭзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com