
 已知,如图,DE⊥AC,BF⊥AC,AD=CB,DE=BF,求证:AB∥DC.
已知,如图,DE⊥AC,BF⊥AC,AD=CB,DE=BF,求证:AB∥DC.科目:初中数学 来源: 题型:
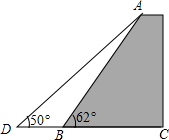 2014年12月31日晚23时35分许,上海外滩陈毅广场发生拥挤踩踏事故.为了排除安全隐患,因此无锡市政府决定改造蠡湖公园的一处观景平台.如图,一平台的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使平台更加牢固,欲改变平台的坡面,使得坡面的坡角∠ADB=50°,则此时应将平台底部向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
2014年12月31日晚23时35分许,上海外滩陈毅广场发生拥挤踩踏事故.为了排除安全隐患,因此无锡市政府决定改造蠡湖公园的一处观景平台.如图,一平台的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使平台更加牢固,欲改变平台的坡面,使得坡面的坡角∠ADB=50°,则此时应将平台底部向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)查看答案和解析>>
科目:初中数学 来源: 题型:
| 2015 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com