
【题目】如图 1,一张△ABC 纸片,点 M、N 分别是 AC、BC 上两点.
(1)若沿直线 MN 折叠,使 C 点落在 BN 上,则∠AMC′与∠ACB 的数量关系是 ;

(2)若折成图 2 的形状.猜想∠AMC′、∠BNC′和∠ACB 的数量关系,并说明理由.
猜想: .
理由:
(3)若折成图3 的形状,猜想∠AMC′、∠BNC′和∠ACB 的数量关系是 .(写出结论即可).
(4)将上述问题推广,如图4,将四边形 ABCD 纸片沿 MN 折叠,使点 C、D 落在四边形 ABNM 的内部时,∠AMD′+∠BNC′与∠C、∠D 之间的数量关系 是 (写出结论即可).

【答案】(1)∠AMC′=2∠ACB;(2)∠AMC′+∠BNC′=2∠ACB,理由见详解;(3)∠AMC′-∠BNC′=2∠ACB;(4)∠AMD′+∠BNC′=2(∠C+∠D)-360°.
【解析】
(1)根据折叠性质和三角形的外角定理得出结论;
(2)先根据折叠得:∠CMN=∠C′MN,∠CNM=∠C′NM,由两个平角∠CMA和∠CNB得:∠AMC′+∠′BNC′等于360°与四个折叠角的差,化简为结果;
(3)利用两次外角定理得∠AMC′=∠C′+∠C+∠BNC′,然后根据等量代换,得出结论;
(4)与(2)类似,先由折叠得:∠DMN=∠D′MN,∠CNM=∠C′NM,再由两平角的和为360°得:∠AMD′+∠BNC′=360°-2∠DMN-2∠CNM,根据四边形的内角和得:∠DMN+∠CNM=360°-∠C-∠D,代入前式可得结论.
解:(1)由折叠得:∠ACB=∠MC′C,
∵∠AMC′=∠ACB+∠MC′C,
∴∠AMC′=2∠ACB;
故答案为:∠AMC′=2∠ACB;
(2)猜想:∠AMC′+∠BNC′=2∠ACB,
理由是:
由折叠得:∠CMN=∠C′MN,∠CNM=∠C′NM,
∵∠CMA+∠CNB=360°,
∴∠AMC′+∠′BNC′=360°-∠CMN-∠C′MN-∠CNM-∠C′NM=360°-2∠CMN-2∠CNM,
∴∠AMC′+∠BNC′=2(180°-∠CMN-∠CNM)=2∠ACB;
(3)∵∠AMC′=∠MDC+∠C,∠MDC=∠C′+∠BNC′,
∴∠AMC′=∠C′+∠BNC′+∠C,
∵∠C=∠C′,
∴∠AMC′=2∠C+∠BNC′,
∴∠AMC′-∠BNC′=2∠ACB;
故答案为:∠AMC′-∠BNC′=2∠ACB;
(4)由折叠得:∠DMN=∠D′MN,∠CNM=∠C′NM,
∵∠DMA+∠CNB=360°,
∴∠AMD′+∠BNC′=360°-2∠DMN-2∠CNM,
∵∠DMN+∠CNM=360°-∠C-∠D,
∴∠AMD′+∠BNC′=360°-2(360°-∠C-∠D)=2(∠C+∠D)-360°,
故答案为:∠AMD′+∠BNC′=2(∠C+∠D)-360°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】珍珍与环环两人一起做游戏,游戏规则如下:每人从1,2,3,4,5,6,7,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于她们各自选择的数,就再做一次上述游戏,直到决出胜负.若环环事先选择的数是5,用列表法或画树状图的方法,求她获胜的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点 O 按如图方式叠放在一起.

( 1 ) 如图 1 , 若∠ BOD=35° , 则∠ AOC= ; 若∠AOC=135°, 则∠BOD= ;
(2)如图2,若∠AOC=140°,则∠BOD= ;
(3)猜想∠AOC 与∠BOD 的大小关系,并结合图1说明理由.
(4)三角尺 AOB 不动,将三角尺 COD 的 OD 边与 OA 边重合,然后绕点 O 按顺时针或逆时针方向任意转动一个角度,当∠A OD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD 角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
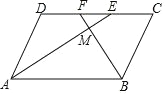
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.下列说法不正确的是( )

A.与∠1互余的角只有∠2B.∠A与∠B互余
C.∠1=∠BD.若∠A=2∠1,则∠B=30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com