
【题目】如图,把![]() 绕着点
绕着点![]() 顺时针方向旋转角度
顺时针方向旋转角度![]() (
(![]() ),得到
),得到![]() ,若
,若![]() ,
,![]() ,
,![]() 三点在同一条直线上,
三点在同一条直线上,![]() ,则
,则![]() 的度数是___________.
的度数是___________.

科目:初中数学 来源: 题型:
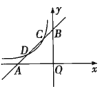
【题目】如图,已知直线![]() 与x轴、y轴分别交于点A,B,与双曲线
与x轴、y轴分别交于点A,B,与双曲线![]() 分别交于点C,D,且点C的坐标为
分别交于点C,D,且点C的坐标为![]() .
.
(1)分别求出直线、双曲线的函数表达式.
(2)求出点D的坐标.
(3)利用图象直接写出:当x在什么范围内取值时![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx﹣2m(m是常数),顶点为P.
(Ⅰ)当抛物线经过点A时,求顶点P的坐标;
(Ⅱ)若点P在x轴下方,当∠AOP=45°时,若函数值y>0,求对应自变量x的取值范围;
(Ⅲ)无论m取何值,该抛物线都经过定点H.当∠AHP=45°时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
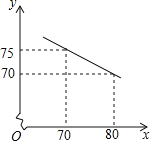
【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的点![]() 处引同样长度的拉线
处引同样长度的拉线![]() ,
,![]() 固定电线杆
固定电线杆![]() ,在离电线杆6米处安置测角仪
,在离电线杆6米处安置测角仪![]() (其中点
(其中点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上),在
在同一条直线上),在![]() 处测得电线杆上点
处测得电线杆上点![]() 处的仰角为
处的仰角为![]() ,测角仪
,测角仪![]() 的高为
的高为![]() 米.
米.
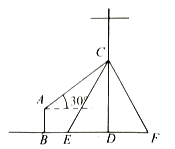
(1)求电线杆上点![]() 离地面的距离
离地面的距离![]() ;
;
(2)若拉线![]() ,
,![]() 的长度之和为18米,求固定点
的长度之和为18米,求固定点![]() 和
和![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
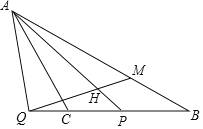
【题目】如图,已知等腰△ABC,∠ACB=120°,P是线段CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得∠PAC=∠QAC,过点Q作射线QH交线段AP于H,交AB于点M,使得∠AHQ=60°.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示);
(2)用等式表示线段QC和BM之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
A 类 | 50 | 25 |
B 类 | 200 | 20 |
C 类 | 400 | 15 |
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com