练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，反比例函数y的图象经过点P（3，4）．

    （1）求k的值；

    （2）求OP的长；

    （3）直线y＝mx（m≠0）与反比例函数的图象有两个交点A，B，若AB＞10，直接写出m的取值范围．

    【答案】（1）k＝12，（2）OP＝5；（3）或．

    【解析】

    （1）根据待定系数法即可求得；

    （2）根据勾股定理即可求得；

    （3）由（2）可知，当A（﹣3，﹣4），B（3，4）或A（﹣4，﹣3），B（4，3）时，AB＝10，m或m，根据AB＞10，即可得到m的取值．

    解：（1）∵反比例函数的图象经过点P（3，4），

    ∴k＝12，

    （2）过点P作PE⊥x轴于点E．

    ∵点P（3，4），

    ∴OE＝3，PE＝4．

    ∴在Rt△EOP中，由勾股定理可求OP＝5；

    （3）由（2）可知，当A（﹣3，﹣4），B（3，4）或A（﹣4，﹣3），B（4，3）时，AB＝10，m或m

    若AB＞10，则或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝ax2+bx+c（a≠0），经过点（1.0），对称轴l如图所示，若M＝a+b﹣c，N＝2a﹣b，P＝a+c，则M，N，P中，值小于0的数有（　　）个．

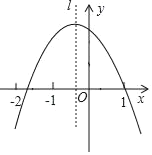
    A.2B.1C.0D.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

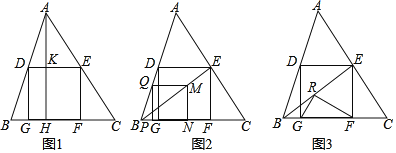
    【题目】在△ABC中，BC＝6，S△ABC＝18，正方形DEFG的边FG在BC上，顶点D，E分别在AB，AC上．

    （1）如图1，过点A作AH⊥BC于点H，交DE于点K，求正方形DEFG的边长；

    （2）如图2，在BE上取点M，作MN⊥BC于点N，MQ∥DE交AB于点Q，QP⊥BC于点P，求证：四边形MNPQ是正方形；

    （3）如图3，在BE上取点R，使RE＝FE，连结RG，RF，若tan∠EBF＝．求证：∠GRF＝90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠ACB＝90°，AC＝1，记∠ABC＝α，点D为射线BC上的动点，连接AD，将射线DA绕点D顺时针旋转α角后得到射线DE，过点A作AD的垂线，与射线DE交于点P，点B关于点D的对称点为Q，连接PQ．

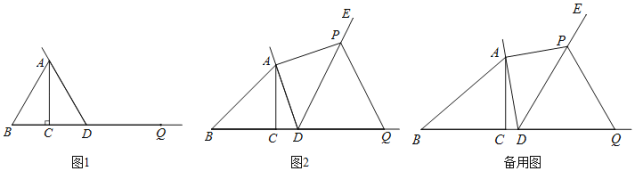
    （1）当△ABD为等边三角形时，

    ①依题意补全图1；

    ②PQ的长为　 　；

    （2）如图2，当α＝45°，且BD＝时，求证：PD＝PQ；

    （3）设BC＝t，当PD＝PQ时，直接写出BD的长．（用含t的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司生产的一种产品按照质量由高到低分为A，B，C，D四级，为了增加产量、提高质量，该公司改进了一次生产工艺，使得生产总量增加了一倍．为了解新生产工艺的效果，对改进生产工艺前、后的四级产品的占比情况进行了统计，绘制了如下扇形图：

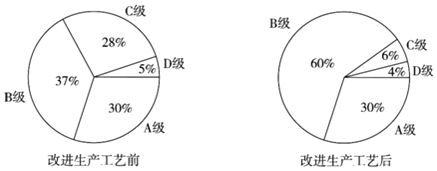
    根据以上信息，下列推断合理的是（　　）

    A.改进生产工艺后，A级产品的数量没有变化

    B.改进生产工艺后，B级产品的数量增加了不到一倍

    C.改进生产工艺后，C级产品的数量减少

    D.改进生产工艺后，D级产品的数量减少

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】M（﹣1，），N（1，）是平面直角坐标系xOy中的两点，若平面内直线MN上方的点P满足：45°≤∠MPN≤90°，则称点P为线段MN的可视点．

    （1）在点，，，A4（2，2）中，线段MN的可视点为　 　；

    （2）若点B是直线y＝x上线段MN的可视点，求点B的横坐标t的取值范围；

    （3）直线y＝x+b（b≠0）与x轴交于点C，与y轴交于点D，若线段CD上存在线段MN的可视点，直接写出b的取值范围．

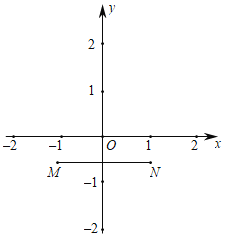
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中(如图)，已知抛物线y=ax2+4ax+c(a≠0)经过A(0，4)，B(﹣3，1)，顶点为C．

    (1)求该抛物线的表达方式及点C的坐标；

    (2)将(1)中求得的抛物线沿y轴向上平移m(m＞0)个单位，所得新抛物线与y轴的交点记为点D．当△ACD时等腰三角形时，求点D的坐标；

    (3)若点P在(1)中求得的抛物线的对称轴上，联结PO，将线段PO绕点P逆时针转90°得到线段PO′，若点O′恰好落在(1)中求得的抛物线上，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

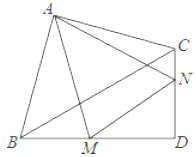
    【题目】如图，在Rt△ABC和Rt△BCD中，∠BAC＝∠BDC＝90°，BC＝4，AB＝AC，∠CBD＝30°，M，N分别在BD，CD上，∠MAN＝45°，则△DMN的周长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

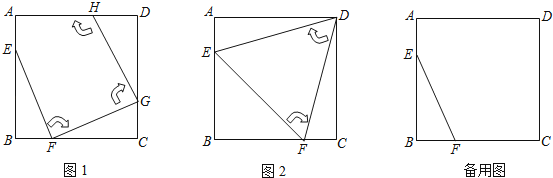
    【题目】如图1，边长为4的正方形ABCD中，点E在AB边上(不与点A，B重合)，点F在BC边上(不与点B、C重合)．

    第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G；

    第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；

    依此操作下去…

    (1)图2中的△EFD是经过两次操作后得到的，其形状为　 　，求此时线段EF的长；

    (2)若经过三次操作可得到四边形EFGH．

    ①请判断四边形EFGH的形状为　 　，此时AE与BF的数量关系是　 　；

    ②以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x的函数关系式及面积y的取值范围．

    查看答案和解析>>

    同步练习册答案