
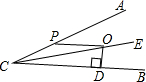
 已知∠ACB的角平分线CE,O是CE上一点,OP∥BC,PO=2,OD⊥CB于D,∠ACE=15°,则OD的长是( )
已知∠ACB的角平分线CE,O是CE上一点,OP∥BC,PO=2,OD⊥CB于D,∠ACE=15°,则OD的长是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
科目:初中数学 来源: 题型:解答题
 如图,某校九年级课外活动小组,在测量树高的一次活动中,测得树底部中心A到斜坡底C的水平距离为8m,在阳光下某一时刻测得1m场的标杆影长是0.5m,同时树影落在斜坡上的部分CD=4m,已知斜坡CD的坡比i=1:$\sqrt{3}$,求树高AB.(结果保留根号)
如图,某校九年级课外活动小组,在测量树高的一次活动中,测得树底部中心A到斜坡底C的水平距离为8m,在阳光下某一时刻测得1m场的标杆影长是0.5m,同时树影落在斜坡上的部分CD=4m,已知斜坡CD的坡比i=1:$\sqrt{3}$,求树高AB.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,每个小正方形的变成都是1厘米,现有一半径为1厘米的圆沿着图形内测运动,如果此圆作旋转(无滑动的滚动)运动,则它经过部分的面积是(34+$\frac{7}{2}π$)平方厘米.(答案保留π)
如图所示,每个小正方形的变成都是1厘米,现有一半径为1厘米的圆沿着图形内测运动,如果此圆作旋转(无滑动的滚动)运动,则它经过部分的面积是(34+$\frac{7}{2}π$)平方厘米.(答案保留π)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数x(cm) | 175 | 173 | 175 | 174 |
| 方差S2(cm2) | 3.5 | 3.5 | 12.5 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com