
 如图,某校九年级课外活动小组,在测量树高的一次活动中,测得树底部中心A到斜坡底C的水平距离为8m,在阳光下某一时刻测得1m场的标杆影长是0.5m,同时树影落在斜坡上的部分CD=4m,已知斜坡CD的坡比i=1:$\sqrt{3}$,求树高AB.(结果保留根号)
如图,某校九年级课外活动小组,在测量树高的一次活动中,测得树底部中心A到斜坡底C的水平距离为8m,在阳光下某一时刻测得1m场的标杆影长是0.5m,同时树影落在斜坡上的部分CD=4m,已知斜坡CD的坡比i=1:$\sqrt{3}$,求树高AB.(结果保留根号) 分析 延长BD与AC的延长线交于点E,过点D作DH⊥AE于点H,由题意可得CH、DH、HE的长度,从而可以求得AE的长,然后根据在阳光下某一时刻测得1m场的标杆影长是0.5m,可以求得AB的长.
解答 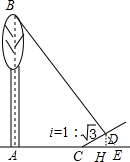 解:如图,延长BD与AC的延长线交于点E,过点D作DH⊥AE于点H,
解:如图,延长BD与AC的延长线交于点E,过点D作DH⊥AE于点H,
∵i=tan∠DCH=$\frac{DH}{CH}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠DCH=30°,
∴DH=$\frac{1}{2}$CD=2(m),CH=$\sqrt{3}$DH=2$\sqrt{3}$(m),
由题意可知,$\frac{DH}{HE}$=1:0.5=2,
∴HE=1(m),
∴AE=AC+CH+HE=8+2$\sqrt{3}$+1=9+2$\sqrt{3}$(m),
∵$\frac{AB}{AE}$=1:0.5=2,
∴AB=2AE=18+4$\sqrt{3}$(m),
即树高AB是$(18+4\sqrt{3})$m.
点评 本题考查解直角三角形-坡度坡角问题,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
 如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为a:b,则$\frac{4a+3}{2b+6}$=$\frac{1}{2}$.
如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为a:b,则$\frac{4a+3}{2b+6}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-(x-y+2z)=x2-x+y+2z | B. | x-(-2x+3y-1)=x+2x+3y+1 | ||
| C. | 3x+2(x-2y+1)=3x-2x-2y-2 | D. | -(x-2)-2(x2+2)=-x+2-2x2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义:如图,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长.
定义:如图,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
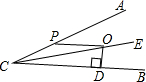 已知∠ACB的角平分线CE,O是CE上一点,OP∥BC,PO=2,OD⊥CB于D,∠ACE=15°,则OD的长是( )
已知∠ACB的角平分线CE,O是CE上一点,OP∥BC,PO=2,OD⊥CB于D,∠ACE=15°,则OD的长是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com