

分析 (1)根据CD平分∠ACE,那么可得∠DCE=45°,进而求得∠BCF是45°,那么CE平分∠BCD.
(2)由∠DCE=35°可先求出∠ACD=55°,再结合∠ACB=∠DCB+∠ACD,∠BCD=90°即可求解.
同理,由∠ACB=140°,可先求出∠ACD从而求出∠DCE.
(3)根据周角定义,再结合已知条件,可以得出∠ACB+∠DCE=180°.
(4)根据角的和差定义,求出∠EAB,再求出∠BAD.
解答 解:(1)∵CD平分∠ACE,∠ACE=90°,
∴∠ACD=∠DCE=45°,
∵∠DCB=90°,
∴∠ECB=90°-∠DCE=45°
∴∠DCE=∠ECB,
∴CE平分∠DCB,
故答案为是.
(2)①∵∠ACD+∠DCE=90°,∠DCE=35°,
∴∠ACD=55°,
∴∠ACB=∠DCB+∠ACD=90°+55°=145°;
②∵∠ACB=140°,
∴∠ACD=∠ACB-∠DCB=50°,
∴∠DCE=∠ACE-∠ACD=40°.
故答案分别为145°、40°.
(3)结论∠ACB+∠DCE=180°
成立.
理由∵∠ACE+∠DCB=180°,
又∵∠ACB+∠DCE+∠ACE+∠DCB=360°,
∴∠ACB+∠DCE=360°-(∠ACE+∠DCB)=180°.
(4)∵∠CAE=100°∠CAB=60°,
∴∠BAE=∠CAE-∠CAB=40°,
∠BAD=∠EAD-∠BAE=60°-40°=20°.
点评 本题考查了角的互余和角的互补的性质以及角的和差定义.周角的定义,正确认识三角板的角的度数,是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一点,连结AD,将线段AD绕点A逆时针旋转一定角度得到线段AE使∠BAD=∠CAE(E在AC右侧),连结BD,CE.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一点,连结AD,将线段AD绕点A逆时针旋转一定角度得到线段AE使∠BAD=∠CAE(E在AC右侧),连结BD,CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
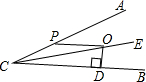 已知∠ACB的角平分线CE,O是CE上一点,OP∥BC,PO=2,OD⊥CB于D,∠ACE=15°,则OD的长是( )
已知∠ACB的角平分线CE,O是CE上一点,OP∥BC,PO=2,OD⊥CB于D,∠ACE=15°,则OD的长是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,3,4 | B. | 4,5,6 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 2,$\sqrt{3}$,$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在一条笔直公路p的两侧,分别有甲、乙两个村庄,现要在公路p上建一个汽车站,使汽车站到甲、乙两村的距离之和最小,你认为汽车站应该建在B处(填A或B或C),理由是两点之间线段最短.
如图所示,在一条笔直公路p的两侧,分别有甲、乙两个村庄,现要在公路p上建一个汽车站,使汽车站到甲、乙两村的距离之和最小,你认为汽车站应该建在B处(填A或B或C),理由是两点之间线段最短.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com