
分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:方程变形得:$\frac{1}{x(x-1)}$+$\frac{1}{x(x+1)}$+$\frac{1}{(x+1)(x+2)}$-$\frac{4}{(x-1)(x+3)}$=0,
即$\frac{1}{x-1}$-$\frac{1}{x}$+$\frac{1}{x}$-$\frac{1}{x+1}$+$\frac{1}{x+1}$-$\frac{1}{x+2}$-$\frac{1}{x-1}$+$\frac{1}{x+3}$=0,
整理得:$\frac{1}{x+3}$-$\frac{1}{x+2}$=0,
去分母得:x+2-x-3=0,即-1=0,矛盾,
则此分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,A、B、C分别为数轴上的三点,A点对应的数为-200,B点对应的数为-20,C点对应的数为40.甲从C点出发,以6单位/秒的速度向左运动.
已知,如图,A、B、C分别为数轴上的三点,A点对应的数为-200,B点对应的数为-20,C点对应的数为40.甲从C点出发,以6单位/秒的速度向左运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
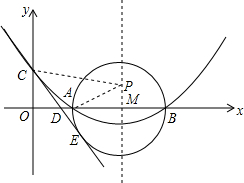 如图,已知抛物线的对称轴为直线l:x=4,且与x轴交于点A(2,0),与y轴交于点C(0,2).
如图,已知抛物线的对称轴为直线l:x=4,且与x轴交于点A(2,0),与y轴交于点C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
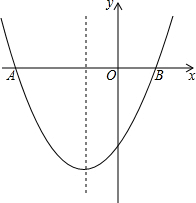 已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-2,与x轴交于A、B两点,与y轴交于点C,其中A(-6,0),C(0,-4).
已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-2,与x轴交于A、B两点,与y轴交于点C,其中A(-6,0),C(0,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
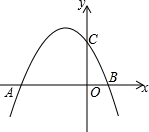 如图,抛物线y=-$\frac{3}{8}{x}^{2}-\frac{3}{4}x+3$与x轴交于A,B两点,与y轴交于点C.
如图,抛物线y=-$\frac{3}{8}{x}^{2}-\frac{3}{4}x+3$与x轴交于A,B两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
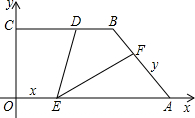 如图,直角梯形OABC的直角顶点O是坐标原点,PA,OC分别在x轴、y轴正半轴上,OA∥BC,D是BC上一点,BD=$\frac{1}{4}OA$=$\sqrt{2}$,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
如图,直角梯形OABC的直角顶点O是坐标原点,PA,OC分别在x轴、y轴正半轴上,OA∥BC,D是BC上一点,BD=$\frac{1}{4}OA$=$\sqrt{2}$,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com