
����Ŀ������ѧУ���Ƽ����սڡ��ڼ䣬���꼶��ѧ�С��������Dz���ѧУ���AB�ĸߣ������������ǰ��̨���ϵĵ�C���������˶���A������Ϊ45�㣬������˵ķ����ߵ�̨���µĵ�F���������˶���A������Ϊ60�㣬��֪����̨�ĸ߶�BEΪ1�ף���C�����ĸ߶�CDΪ3�ף�̨��CF���½�Ϊ30�㣬�ҵ�E��F��D��ͬһ��ֱ���ϣ������AB�ĸ߶ȣ���������ȷ��0.1�ף��ο����ݣ� ![]() ��1.41��
��1.41�� ![]() ��1.73��
��1.73��
���𰸡��⣺����C��CM��AB��M�����ı���MEDC�Ǿ��Σ�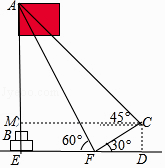
��ME=DC=3��CM=ED��
��Rt��AEF�У���AFE=60�㣬��EF=x����AF=2x��AE= ![]() x��
x��
��Rt��FCD�У�CD=3����CFD=30�㣬
��DF=3 ![]() ��
��
��Rt��AMC�У���ACM=45�㣬
���MAC=��ACM=45�㣬
��MA=MC��
��ED=CM��
��AM=ED��
��AM=AE��ME��ED=EF+DF��
�� ![]() x��3=x+3
x��3=x+3 ![]() ��
��
��x=6+3 ![]() ��
��
��AE= ![]() ��6+3
��6+3 ![]() ��=6
��=6 ![]() +9��
+9��
��AB=AE��BE=9+6 ![]() ��1��18.4�ף�
��1��18.4�ף�
�����AB�ĸ߶�ԼΪ18.4�ף�
������������C��CM��AB��M�����ı���MEDC�Ǿ��Σ���EF=x������AM=DE���г����̼��ɽ�����⣮
�����㾫����ͨ��������ù������Ǹ������⣬�������ǣ�������ˮƽ���Ϸ��Ľǣ����ǣ�������ˮƽ���·��ĽǼ����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��ӳ�AB��E���ӳ�CD��F��BE=DF������EF����BC��AD�ֱ��ཻ��P��Q���㣮
��1����֤��CP=AQ��
��2����BP=1��PQ=![]() ����AEF=45���������ABCD�������
����AEF=45���������ABCD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ų����ε����ӿ���6�ˣ�����ͼ������ƴ������

��������������ȥ����1����5������ʱ������ ���ˣ�
��2����10������ʱ������ ���ˣ�
��3����n�����ӿ������� ���ˣ��ú���n�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�����߷ֱ����DEF������ƽ�У���BA��ED��BC��EF��

��1����ͼ1�У�����BA��EDͬ��BC��EFҲͬ��B���E��������ϵ�ǣ� ��
��2����ͼ2�У�����BA��ED����BC��EFҲ����B���E��������ϵ�ǣ� ��
��3����ͼ3�У�����BA��EDͬ��BC��EF����B���E��������������ϵ����˵�����ɣ�
��4��ͨ�����棨1������2������3������ɵõ��Ľ����ǣ����һ���ǵ����߷ֱ�ƽ������һ���ǵ����ߣ����������ǵĹ�ϵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
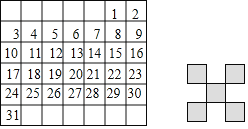
����Ŀ����ͼ��ij�µ�����������ͼǡ������ȫ�ڸ�ס�������е�������֣������Ӱ����![]() �����е�5�����ֵ���С��Ϊa��
�����е�5�����ֵ���С��Ϊa��
![]() ���ú�a�Ĵ���ʽ��ʾ��5������
���ú�a�Ĵ���ʽ��ʾ��5������
![]() ������������
��������ĺ�����![]() �������ĵ�����ʲô��ϵ��
�������ĵ�����ʲô��ϵ��
![]() ��ס��5�����ֵĺ���Ϊ105��Ϊʲô��
��ס��5�����ֵĺ���Ϊ105��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��cΪ�����ʵ������![]() �Ŀ���ֵ�ĸ���Ϊ��������
�Ŀ���ֵ�ĸ���Ϊ��������
A. 4 B. 5 C. 6 D. 7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2����״��С��ȫ��ͬ��С�����ο�Ƭ����ͼ�٣����ص��ط���һ������Ϊ�����Σ���Ϊm����Ϊn���ĺ��ӵײ�����ͼ�ڣ������ӵ���δ����Ƭ���ǵIJ�������Ӱ��ʾ����Ӱ���ָպ��ָܷ��������״��С��ͬ��С�����ο�Ƭ����ͼ�ۣ�����ָ���������Ӱ�����ε��ܳ����ǣ�������
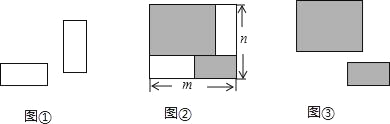
A. 4mB. 2��m+n��C. 4nD. 4��m��n��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ�������һ������Ϊa1����2������Ϊa2����3������Ϊa3����������n������Ϊan����a1����![]() ���ӵڶ�������ÿһ�������ǡ�1������ǰ���Ǹ����IJ�ĵ�����
���ӵڶ�������ÿһ�������ǡ�1������ǰ���Ǹ����IJ�ĵ�����
��1��ֱ��д��a2��a3��a4��ֵ��
��2���������Ͻ��������a1+a2+a3+��+a2017+a2018��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������˵���в���ȷ���ǣ�������

A. ��1���AOB��ͬһ����B. ��AOCҲ�����á�O��ʾ
C. ��������BOCD. ͼ����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com