
【题目】(1)如图,若大正方形的边长为a,小正方形的边长为b,则阴影部分的面积是 ;若如图中的阴影部分剪下来,重新拼叠成如图的一个矩形,则它长为 ;宽为 ;面积为 .
(2)由(1)可以得到一个公式: .
(3)利用你得到的公式计算:20192﹣2018×2020.

【答案】(1)a2﹣b2,a+b,a﹣b,(a+b)(a﹣b);(2)(a+b)(a﹣b)=a2﹣b2;(3)1.
【解析】
(1)利用正方形的面积公式,图1阴影部分的面积为大正方形的面积-小正方形的面积,图2长方形的长为a+b,宽为a-b,利用长方形的面积公式可得结论;
(2)由(1)建立等量关系即可;
(3)根据平方差公式进行计算即可.
解:(1)图①阴影部分的面积为:a2﹣b2,图②长方形的长为a+b,宽为a﹣b,所以面积为:(a+b)(a﹣b),
故答案为:a2﹣b2,a+b,a﹣b,(a+b)(a﹣b);
(2)由(1)可得:(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b)=a2﹣b2;
(3)20192﹣2018×2020,
=20192﹣(2019+1)(2019﹣1),
=20192﹣20192+1,
=1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D ,点E为线段BC的中点,AD=2,tan A=2.
(1)求AB的长;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1 . 
(1)在图中画出△A1B1C1;
(2)点A1 , B1 , C1的坐标分别为、、;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )
A.2![]() ﹣2
﹣2
B.6
C.2![]() ﹣2
﹣2
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,OP平分∠AOB,PC∥OB交OA于点C,PD⊥OB于点D,如果PC=6,那么PD的长是_________________.
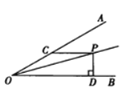
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A、B、C三点的坐标分别为(﹣2,4)、(﹣3,0)、(4,1).
(1)画出△ABC;
(2)△ABC的面积为 ;
(3)△ABC向上平移3个单位长度,向左平移1个单位长度.请画出图形并写出对应点A1B1C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为 . 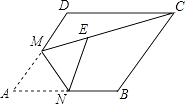
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)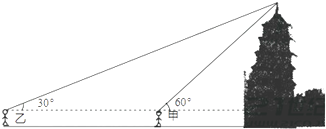
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根.
(2)是否存在实数k使方程两根的倒数和为2?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com