Question

15．一个三角形可被分成两个等腰三角形，原三角形的一个内角的36°，则原三角形最大内角的所有可能值为72°或90°或108°或126°或132°．

Answer 1

分析 分为以下情况：
①原三角形是锐角三角形，最大角是72°的情况；
②原三角形是直角三角形，最大角是90°的情况；
③原三角形是钝角三角形，最大角是108°的情况；
④原三角形是钝角三角形，最大角是126°的情况；
⑤原三角形是钝角三角形，最大角是132°的情况．

解答 解：①原三角形是锐角三角形，最大角是72°的情况：
如图∠ABC=∠ACB=72°，∠A=36°，AD=BD=BC，则最大角是72°；
，
②原三角形是直角三角形，最大角是90°的情况：
如图∠ABC=90°，∠A=36°，AD=CD=BD，；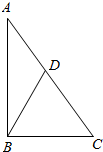

③原三角形是钝角三角形，最大角是108°的情况：
如图∠BAC=108°，∠B=36°，BD=AB，AD=DC，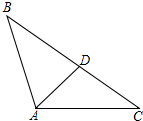

④原三角形是钝角三角形，最大角是126°的情况：
如图∠ABC=126°，∠C=36°，AD=BD=BC，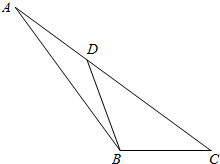

⑤原三角形是钝角三角形，最大角是132°的情况：
如图∠C=132°，∠ABC=36°，AD=BD，CD=CB，

故答案为：72°或90°或108°或126°或132°

点评 本题主要考查了等腰三角形的性质及三角形内角和定理；分情况讨论是解决本题的关键，本题有一定的难度，大部分学生思考没那么全面．