
【题目】新房装修后,某居民购买家用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
垃圾桶 | 15 | ||
鞋架 | 40 | ||
字画 | a | 2 | 90 |
合计 | 5 | 185 | |
(1)居民购买垃圾桶,鞋架各几个?
(2)若居民再次购买字画和垃圾桶两种家居用品共花费150元,则有哪几种不同的购买方案?
【答案】(1)居民购买垃圾桶1个,鞋架2个(2)有三种不同的购买方案
【解析】试题分析:(1)设居民购买垃圾桶x个,鞋架y个,找出数量和金额的等量关系,列方程组求解即可.
(2)设购买字画a个,购买垃圾桶b个,先求出字画的单价,根据购买字画和垃圾桶两种家居用品共花费150元,列出式子![]() ,化简得
,化简得![]() 求出方程的正整数解即可.
求出方程的正整数解即可.
试题解析:(1)设居民购买垃圾桶x个,鞋架y个,
则![]()
解得: ![]()
答:居民购买垃圾桶1个,鞋架2个;
(2)设购买字画a个,购买垃圾桶b个,
字画单价为90÷2=45,
则![]()
![]()
当a=1时,b=7,
当a=2时,b=4,
当a=3时,b=1,
即有三种不同的购买方案:
第一种方案是:购买字画1个,购买垃圾桶7个;
第二种方案是:购买字画2个,购买垃圾桶4个;
第三种方案是:购买字画3个,购买垃圾桶1个.


科目:初中数学 来源: 题型:
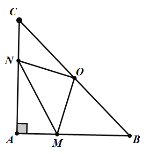
【题目】如图在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系.
(2)如果点M、N分别在线段AB、AC上移动,移动中保持AN=BM,请判断△OMN的形状,并证明你的结论.
(3)当点M、N分别在AB、AC上运动时,四边形AMON的面积是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
①打电话时,小刚和妈妈的距离为1250米;
②打完电话后,经过23分钟小刚到达学校;
③小刚和妈妈相遇后,妈妈回家的速度为150米/分;
④小刚家与学校的距离为2550米.其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)![]() (x﹣5)=3﹣
(x﹣5)=3﹣![]() (x﹣5)
(x﹣5)
(3)![]() ﹣1=
﹣1=![]()
(4)x﹣![]() (x﹣9)=
(x﹣9)=![]() [x+
[x+![]() (x﹣9)]
(x﹣9)]
(5) ![]() -
-![]() =0.5x+2
=0.5x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨 ![]() .下表是去年该酒店豪华间某两天的相关记录:
.下表是去年该酒店豪华间某两天的相关记录:
淡季 | 旺季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24000 | 40000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元?
(2)今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(-1)3-![]() ×[2-(-3)2]
×[2-(-3)2]
(2) 计算:(﹣12)+(+30)﹣(+65)﹣(﹣47)
(3) 计算:39![]() ×(﹣12)
×(﹣12)
(4) 计算:(﹣1000)×(![]() ﹣
﹣![]() +
+![]() ﹣0.1)
﹣0.1)
(5)化简:﹣4(a3﹣3b)+(﹣2b2+5a3)
(6)化简:2a﹣2(﹣0.5a+3b﹣c)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律: ①该蔬菜的销售价P(单位:元/千克)与时间x(单位:月份)满足关系:P=9﹣x
②该蔬菜的平均成本y(单位:元/千克)与时间x(单位:月份)满足二次函数关系y=ax2+bx+10,已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润L(单位:元/千克)最大?最大平均利润是多少?(注:平均利润=销售价﹣平均成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2 . 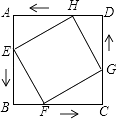
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com