
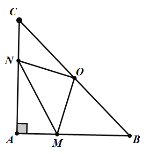
【题目】如图在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系.
(2)如果点M、N分别在线段AB、AC上移动,移动中保持AN=BM,请判断△OMN的形状,并证明你的结论.
(3)当点M、N分别在AB、AC上运动时,四边形AMON的面积是否发生变化?说明理由.
【答案】(1) OA=OB=OC;(2)等腰三角形;(3)不变.
【解析】
(1)由于△ABC是直角三角形,点O是BC的中点,根据直角三角形的性质:直角三角形斜边上的中线等于斜边的一半,故有OA=OB=OC=![]() BC;
BC;
(2)由于OA是等腰直角三角形的斜边上的中线,根据等腰直角三角形的性质知,∠CAO=∠B=45°,OA=OB,又有AN=MB,所以由SAS证得△AON≌△BOM可得:ON=OM ①∠NOA=∠MOB,于是有,∠NOM=∠AOB=90°,所以△OMN是等腰直角三角形.
(3)由全等三角形的面积相等和图中图形间的面积关系得到.
(1)∵在Rt△ABC中,∠BAC=90°,O为BC的中点,
∴OA=![]() BC=OB=OC,
BC=OB=OC,
即OA=OB=OC;
(2)△OMN是等腰直角三角形.理由如下:
连接AO
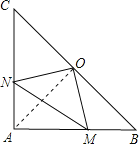
∵AC=AB,OC=OB
∴OA=OB,∠NAO=∠B=45°,
在△AON与△BOM中,
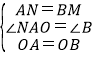 ,
,
∴△AON≌△BOM(SAS)
∴ON=OM,∠NOA=∠MOB
∴∠NOA+∠AOM=∠MOB+∠AOM
∴∠NOM=∠AOB=90°,
∴△OMN是等腰直角三角形;
(3)当点M、N分别在AB、AC上运动时,四边形AMON的面积不发生变化.理由如下:
M、N运动时始终有△AON≌△BOM,
故S四边形AMON=SAMO+SMBO=SABO=![]() SABC.
SABC.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分面积用2种方法表示可得一个等式,这个等式为_______.
(2)若(4x﹣y)2=9,(4x+y)2=169,求xy的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,(1)∠BED与∠CBE是直线________,________被直线________所截形成的________角;
(2)∠A与∠CED是直线________,________被直线________所截形成的________角;
(3)∠CBE与∠BEC是直线________,________被直线________所截形成的________角;
(4)∠AEB与∠CBE是直线________,________被直线________所截形成的________角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣2,﹣1),B(﹣4,1),C(﹣3,3).△ABC关于原点O对称的图形是△A1B1C1 . 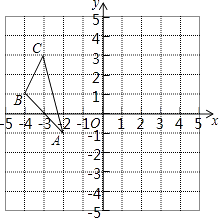
(1)画出△A1B1C1;
(2)BC与B1C1的位置关系是 , AA1的长为;
(3)若点P(a,b)是△ABC 一边上的任意一点,则点P经过上述变换后的对应点P1的坐标可表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新房装修后,某居民购买家用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
垃圾桶 | 15 | ||
鞋架 | 40 | ||
字画 | a | 2 | 90 |
合计 | 5 | 185 | |
(1)居民购买垃圾桶,鞋架各几个?
(2)若居民再次购买字画和垃圾桶两种家居用品共花费150元,则有哪几种不同的购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com