
【题目】甲乙两地相距900千米,一列快车从甲地出发匀速开往乙地,速度为120千米/时;快车开出30分钟时,一列慢车从乙地出发匀速开往甲地,速度为90千米/时.设慢车行驶的时间为x小时,快车到达乙地后停止行驶,根据题意解答下列问题:
(1)当快车与慢车相遇时,求慢车行驶的时间;
(2)请从下列(A),(B)两题中任选一题作答.
(A)当两车之间的距离为315千米时,求快车所行的路程;
(B)①在慢车从乙地开往甲地的过程中,求快慢两车之间的距离;(用含x的代数式表示)
我选择: .
作答:
【答案】
(1)解:设慢车行驶的时间为x小时,由题意得
120(x+ ![]() )+90x=900,
)+90x=900,
解得x=4.
答:当快车与慢车相遇时,慢车行驶了4小时
(2)(A)/(B);(A)当两车之间的距离为315千米时,有两种情况:
①两车相遇前相距315千米,此时120(x+ ![]() )+90x=900﹣315,
)+90x=900﹣315,
解得x=2.5.
120(x+ ![]() )=360(千米);
)=360(千米);
②两车相遇后相距315千米,此时120(x+ ![]() )+90x=900+315,
)+90x=900+315,
解得x=5.5.
120(x+ ![]() )=720(千米);
)=720(千米);
③当快车到达乙地时,快车行驶了7.5小时,慢车行驶了7小时,7×90=630>315,此种情况不存在.
答:当两车之间的距离为315千米时,快车所行的路程为360千米或720千米;
(B)①当慢车与快车相遇前,即0≤x<4时,两车的距离为900﹣120(x+ ![]() )﹣90x=840﹣210x;
)﹣90x=840﹣210x;
当慢车与快车相遇后,快车到达乙地前,即4≤x<7.5时,两车的距离为120(x+ ![]() )+90x﹣900=210x﹣840;
)+90x﹣900=210x﹣840;
当快车到达乙地时,即7.5≤x≤10时,两车的距离为90x;
②若第二列快车也从甲地出发匀速驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇后30分钟时,第二列快车与慢车相遇,直接写出第二列快车比第一列快车晚出发多少小时.
解:在第一列快车与慢车相遇后30分钟时,慢车行驶的时间为4+ ![]() =
= ![]() 小时,快车慢车行驶的时间为4+
小时,快车慢车行驶的时间为4+ ![]() +
+ ![]() =5小时.
=5小时.
设第二列快车行驶y小时与慢车相遇,由题意,得
120y+ ![]() ×90=900,
×90=900,
解得y=4 ![]() ,
,
5﹣4 ![]() =
= ![]() (小时).
(小时).
答:第二列快车比第一列快车晚出发 ![]() 小时
小时
【解析】(1)根据题意可知此题的等量关系是:相遇时,快车行驶的路程+慢车行驶的路程=900,列方程求解即可。
(2)(A)当两车之间的距离为315千米时,分三种情况:①两车相遇前相距315千米,等量关系是:快车行驶的路程+慢车行驶的路程=900-315;②两车相遇后相距315千米,等量关系是:快车行驶的路程+慢车行驶的路程=900+315;③当快车到达乙地时,快车行驶了7.5小时,慢车行驶了7小时,7×90=630>315,此种情况不存在,即可得出结果。
(B)分三种情况:①当慢车与快车相遇前,即0≤x<4时;当慢车与快车相遇后,即4≤x<7.5时;快车到达乙地前,当快车到达乙地时,即7.5≤x≤10时。即可求出结果。


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有两条线段AB和CD , 线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.![]()
(1)填空:点B在数轴上表示的数是 , 点C在数轴上表示的数是;
(2)若线段CD以每秒3个单位的速度向右匀速运动,当点D运动到A时,线段CD与线段AB开始有重叠部分,此时线段CD运动了秒;
(3)在(2)的条件下,线段CD继续向右运动,问再经过秒后,线段CD与线段AB不再有重叠部分;
(4)若线段AB、CD同时从图中位置出发,线段AB以每秒2个单位的速度向左匀速运动,线段CD仍以每秒3个单位的速度向右匀速运动,点P是线段CD的中点,问运动几秒时,点P与线段AB两端点(A或B)的距离为1个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两公司近年销售收入情况的折线统计图,根据统计图得出下列结论,其中正确的是( )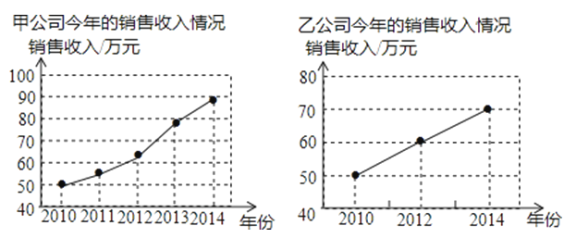
A.甲公司近年的销售收入增长速度比乙公司快
B.乙公司近年的销售收入增长速度比甲公司快
C.甲、乙两公司近年的销售收入增长速度一样快
D.不能确定甲、乙两公司近年销售收入增长速度的快慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)约定“※”为一种新的运算符号,先观察下列各式:
1※3=1×4+3=7;3※(﹣1)=3×4﹣1=11;5※ ![]() =5×4+
=5×4+ ![]() =
= ![]() ;
;
5※4=5×4+4=24;4※(﹣3)=4×4﹣3=13;(﹣ ![]() )※0=(﹣
)※0=(﹣ ![]() )×4+0=﹣
)×4+0=﹣ ![]()
…
根据以上的运算规则,写出a※b= .
(2)根据(1)中约定的a※b的运算规则,求解问题①和②
①若(x﹣3)※x的值等于13,求x的值;
②若2m﹣n=2,请计算:(m﹣n)※(2m+n).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,我们曾经研究过![]() 的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道:
的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道: ![]() …
…![]() 时,我们可以这样做:
时,我们可以这样做:
(1)观察并猜想:
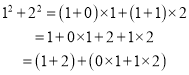 ;
;
![]()
=![]()
=![]() ;
;
![]()
=![]()
=![]() ( );…
( );…
(2)归纳结论:
![]() …
…![]() …
…![]()
=![]() …
…![]()
=( )+[ ]
= +
=![]() .
.
(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com