
【题目】如图1中, ![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿折线
的速度沿折线![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 运动,
运动,![]() 两点同时出发,当某一点运动到点
两点同时出发,当某一点运动到点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ),
),![]() 关于
关于![]() 的函数图象由
的函数图象由![]() 两段组成,如图2所示,有下列结论:①
两段组成,如图2所示,有下列结论:①![]() ;②
;②![]() :③图象
:③图象![]() 段的函数表达式为
段的函数表达式为![]() ;④
;④![]() 面积的最大值为8,其中正确的个数有( )个
面积的最大值为8,其中正确的个数有( )个
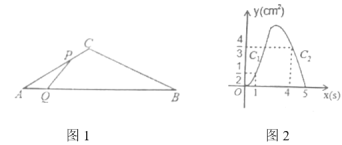
A.1个B.2个C.3个D.4个
【答案】A
【解析】
①根据题意列出y=![]() APAQsinA,即可解答
APAQsinA,即可解答
②根据图像可知PQ同时到达B,则AB=5,AC+CB=10,再代入即可
③把sinB=![]() ,代入解析式即可
,代入解析式即可
④根据题意可知当x=﹣![]() 时,y最大=
时,y最大=![]()
解:①当点P在AC上运动时,y=![]() APAQsinA=
APAQsinA=![]() ×2xvx=vx2,
×2xvx=vx2,
当x=1,y=![]() 时,得v=1,
时,得v=1,
故此选项正确;
②由图象可知,PQ同时到达B,则AB=5,AC+CB=10,
当P在BC上时y=![]() x(10﹣2x)sinB,
x(10﹣2x)sinB,
当x=4,y=![]() 时,代入解得sinB=
时,代入解得sinB=![]() ,
,
故此选项正确;
③∵sinB=![]() ,
,
∴当P在BC上时y=![]() x(10﹣2x)×
x(10﹣2x)×![]() =﹣
=﹣![]() x2+
x2+![]() x,
x,
∴图象C2段的函数表达式为y=﹣![]() x2+
x2+![]() x,
x,
故此选项不正确;
④∵y=﹣![]() x2+
x2+![]() x,
x,
∴当x=﹣![]() 时,y最大=
时,y最大=![]() ,
,
故此选项不正确;
故选:A.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=α,点D在边AC上(不与点A,C重合)连接BD,点K为线段BD的中点,过点D作DE⊥AB于点E,连结CK,EK,CE,将△ADE绕点A顺时针旋转一定的角度(旋转角小于90°)

(1)如图1,若α=45°,则△ECK的形状为______;
(2)在(1)的条件下,若将图1中的△ADE绕点A旋转,使得D,E,B三点共线,点K为线段BD的中点,如图2所示,求证:BE-AE=2CK;
(3)若△ADE绕点A旋转至图3位置时,使得D,E,B三点共线,点K仍为线段BD的中点,请你直接写出BE,AE,CK三者之间的数量关系(用含α的三角函数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:CE=CB.
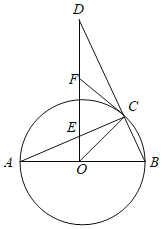
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 140元 B. 150元 C. 160元 D. 180元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,边
,边![]() 的长为
的长为![]() 边
边![]() 的长为
的长为![]() ,在此三角形内有一个矩形
,在此三角形内有一个矩形![]() ;点
;点![]() 分别在
分别在![]() 上,设
上,设![]() 的长为
的长为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() (单位:
(单位: ![]() )
)
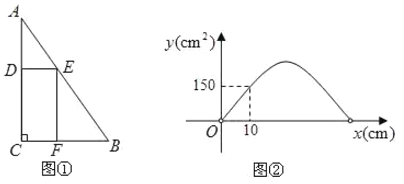
(1)当![]() 等于30时,求
等于30时,求![]() 与
与![]() 的函数关系式:(不要求写出自变量
的函数关系式:(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)在(1)的条件下,矩形![]() 的面积能否为
的面积能否为![]() ?请说明理由?
?请说明理由?
(3)若![]() 与
与![]() 的函数图象如图2所示,求此时
的函数图象如图2所示,求此时![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
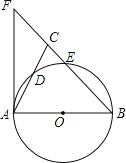
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形EFGH是由四边形ABCD经过旋转得到的,如果用有序数对(3,1)表示方格纸上A点的位置,用(2,2)表示点B的位置,那么由四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示为_____(数为整数)
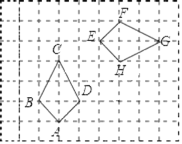
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是半圆![]() 弧上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.下面是小元的探究过程,请补充完整:
弧上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.下面是小元的探究过程,请补充完整:
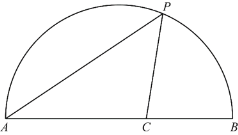
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:

①经测量m的值是(保留一位小数).
②在AP,PC,AC的长度这三个量中,确定 的长度是自变量, 的长度和的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com