练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一人站在两等高的路灯之间走动，为人在路灯照射下的影子，为人在路灯照射下的影子．当人从点走向点时两段影子之和的变化趋势是（ ）

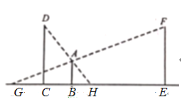
    A.先变长后变短B.先变短后变长

    C.不变D.先变短后变长再变短

    【答案】C

    【解析】

    连接DF，由题意易得四边形CDFE为矩形.由DF∥GH，可得.又AB∥CD，得出，设=a,DF=b（a,b为常数），可得出，从而可以得出，结合可将DH用含a,b的式子表示出来，最后得出结果.

    解：连接DF，已知CD=EF，CD⊥EG,EF⊥EG,

    ∴四边形CDFE为矩形.

    ∴DF∥GH,

    ∴

    又AB∥CD，∴.

    设=a，DF=b,

    ∴,

    ∴

    ∴

    ∴GH=，

    ∵a,b的长是定值不变，

    ∴当人从点走向点时两段影子之和不变．

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

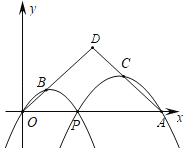
    【题目】如图，已知点A(12，0)，O为坐标原点，P是线段OA上任一点(不含端点O、A).二次函数y1的图象过P、O两点.二次数y2的图象过P、A两点，它的开口均向下，顶点分别为B、C.射线OB与射线AC相交于点D.用当OD＝AD＝9时，这两个二次函数的最大值之和等于______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校决定加强羽毛球，篮球，乒乓球，排球，足球五项球类运动，每位同学必须且只能选择一项运动项目．对全校学生选取进行随机抽样调查，根据调查结果绘制了如下不完整的频数分布表和扇形统计图：

    运动项目

    频数（人数）

    羽毛球

    篮 球

    乒乓球

    排 球

    足 球

    12

    请根据以上图表信息解答下列问题：

    （1）频数分布表中的=　 ，=　 ．

    （2）在扇形统计图中，“羽毛球”所在的扇形的圆心角的度数为　 ；

    （3）全校有多少名学生选择参加篮球运动？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E为边AD上的一点，将△DEC沿CE折叠至△D′EC处，若∠B＝48°，∠ECD＝25°，则∠D′EA的度数为（　　）

    A.33°B.34°C.35°D.36°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有三张正面分别标有数字：-1，1，2的卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽出一张记下数字，放回洗匀后再从中随机抽出一张记下数字．

    (1)请用列表或画树形图的方法（只选其中一种），表示两次抽出卡片上的数字的所有结果；

    (2)将第一次抽出的数字作为点的横坐标x，第二次抽出的数字作为点的纵坐标y，求点（x，y）落在双曲线上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若两个一次函数的图象与x轴交于同一点，则称这两个函数为一对“x牵手函数”，这个交点为“x牵手点”．

    （1）一次函数y＝x﹣1与x轴的交点坐标为　 ；一次函数y＝ax+2与一次函数y＝x﹣1为一对“x牵手函数”，则a＝　 ；

    （2）已知一对“x牵手函数”：y＝ax+1与y＝bx﹣1，其中a，b为一元二次方程x2﹣kx+k﹣4＝0的两根，求它们的“x牵手点”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

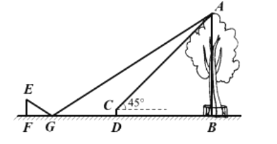
    【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午，他和学习小组的同学带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示。于是他们先在古树周围的空地上选择一点D，并在点D处安装了测量器DC，测得古树的顶端A的仰角为45°；再在BD的延长线上确定一点G，使DG=5米，并在G处的地面上水平放置了一个小平面镜，小明沿着BG方向移动，当移动带点F时，他刚好在小平面镜内看到这棵古树的顶端A的像，此时，测得FG=2米，小明眼睛与地面的距离EF=1.6米，测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上，且EF、CD、AB均垂直于FB，求这棵古树的高度AB。（小平面镜的大小忽略不计）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

    （1）求证：AF=DC；

    （2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．

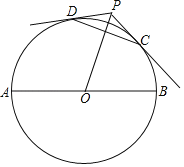
    （1）求证：OP⊥CD；

    （2）连接AD，BC，若∠DAB＝50°，∠CBA＝70°，OA＝2，求OP的长．

    查看答案和解析>>

    同步练习册答案