Question

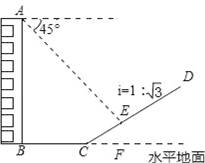
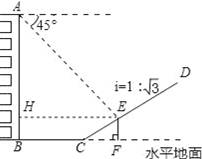
如图，一楼房AB后有一假山，其坡度为i=1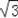：，山坡坡面上E点处有一休息亭，测得假山坡脚C与楼房水平距离BC=25米，与亭子距离CE=20米，小丽从楼房顶测得E点的俯角为45°，求楼房AB的高．（注：坡度i是指坡面的铅直高度与水平宽度的比）

　

Answer 1

【考点】解直角三角形的应用-仰角俯角问题；解直角三角形的应用-坡度坡角问题．

【专题】应用题．

【分析】过点E作EF⊥BC的延长线于F，EH⊥AB于点H，根据CE=20米，坡度为i=1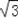：，分别求出EF、CF的长度，在Rt△AEH中求出AH，继而可得楼房AB的高．

【解答】解：过点E作EF⊥BC的延长线于F，EH⊥AB于点H，

在Rt△CEF中，

∵i===tan∠ECF，

∴∠ECF=30°，

∴EF=CE=10米，CF=10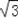米，

∴BH=EF=10米，HE=BF=BC+CF=（25+10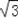）米，

在Rt△AHE中，∵∠HAE=45°，

∴AH=HE=（25+10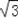）米，

∴AB=AH+HB=（35+10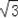）米．

答：楼房AB的高为（35+10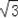）米．

【点评】本题考查了解直角三角形的应用，涉及仰角俯角及坡度坡角的知识，构造直角三角形是解题关键．