
【题目】对于平面直角坐标系![]() 中,已知点A(-2,0)和点B(3,0),线段AB和线段AB外的一点P,给出如下定义:若45°≤∠APB≤90°时,则称点P为线段AB的可视点,且当PA=PB时,称点P为线段AB的正可视点.
中,已知点A(-2,0)和点B(3,0),线段AB和线段AB外的一点P,给出如下定义:若45°≤∠APB≤90°时,则称点P为线段AB的可视点,且当PA=PB时,称点P为线段AB的正可视点.
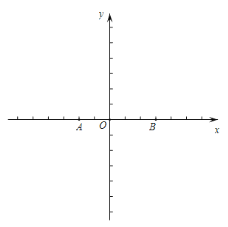
图1 备用图
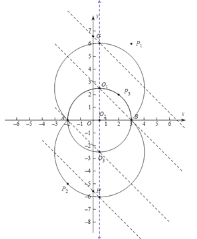
(1) ①如图1,在点P1(3,6),P2(-2,-5),P3(2,2)中,线段AB的可视点是 ;
②若点P在y轴正半轴上,写出一个满足条件的点P的坐标:__________.
(2)在直线y=x+b上存在线段AB的可视点,求b的取值范围;
(3)在直线y=-x+m上存在线段AB的正可视点,直接写出m的取值范围.
【答案】(1)①线段AB的可视点是![]() ,
,![]() ; ②点P的坐标:P(0,3)(答案不唯一,纵坐标
; ②点P的坐标:P(0,3)(答案不唯一,纵坐标![]() 范围:
范围:![]() ≤
≤![]() ≤6);(2)b的取值范围是:-8≤b≤7; (3)m的取值范围:
≤6);(2)b的取值范围是:-8≤b≤7; (3)m的取值范围:![]() 或
或![]()
【解析】
(1)根据题意画出图形,进一步即可得出结论;
(2)正确画出相关图形进一步证明即可;
(3)根据题意,正确画出图形,根据相关量之间的关系进一步求解即可.
(1)①线段AB的可视点是![]() ,
,![]() .
.
②点P的坐标:P(0,3)(答案不唯一,纵坐标![]() 范围:
范围:![]() ≤
≤![]() ≤6).
≤6).
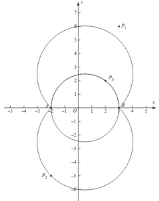
(2)如图,直线与⊙![]() 相切时,BD是⊙
相切时,BD是⊙![]() 直径
直径
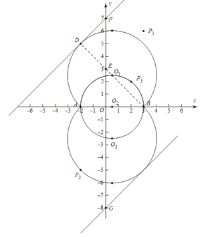
∴BD=![]() .
.
∵BE=![]() ,
,
∴DE=![]() .
.
∴EF=![]() =4.
=4.
∴F(0,7)
同理可得,
直线与⊙![]() 相切时,G(0,-8)
相切时,G(0,-8)
∴b的取值范围是:-8≤b≤7.
(3)m的取值范围:![]() 或
或![]()


科目:初中数学 来源: 题型:
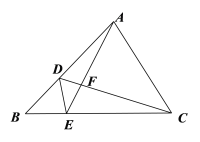
【题目】已知:如图,在△ABC中,点D,E分别在边AB,BC上,BABD=BCBE
(1)求证:△BDE∽△BCA;
(2)如果AE=AC,求证:AC2=ADAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
(1)A点坐标为 ,B点坐标为 ,C点坐标为 ;
(2)如图1,D为B点右侧抛物线上一点,连接AD,若tan∠CAD=2,求D点坐标;
(3)E、F是对称轴右侧第一象限抛物线上的两动点,直线AE、AF分别交y轴于M、N,如图2.若OMON=2,直线EF上有且只有一点P到原点O的距离为定值,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
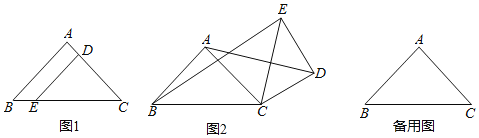
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现:当α=0°时,![]() 的值为 ;
的值为 ;
(2)拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出![]() 的值;
的值;
(3)问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:如图1,昌平南环大桥是经典的悬索桥,当今大跨度桥梁大多采用此种结构.此种桥梁各结构的名称如图2所示,其建造原理是在两边高大的桥塔之间,悬挂着主索,再以相应的间隔,从主索上设置竖直的吊索,与桥面垂直,并连接桥面承接桥面的重量,主索几何形态近似符合抛物线.

图1
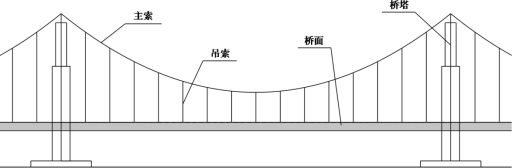
图2
材料2:如图3,某一同类型悬索桥,两桥塔AD=BC=10 m,间距AB为32 m,桥面AB水平,主索最低点为点P,点P距离桥面为2 m;

图3
为了进行研究,甲、乙、丙三位同学分别以不同方式建立了平面直角坐标系,如下图:
甲同学:以DC中点为原点,DC所在直线为x轴,建立平面直角坐标系;

乙同学:以AB中点为原点,AB所在直线为x轴,建立平面直角坐标系;

丙同学:以点P为原点,平行于AB的直线为x轴,建立平面直角坐标系.
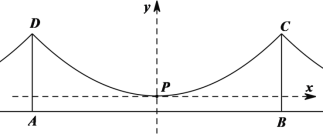
(1)请你选用其中一位同学建立的平面直角坐标系,写出此种情况下点C的坐标,并求出主索抛物线的表达式;
(2)距离点P水平距离为4 m和8 m处的吊索共四条需要更换,则四根吊索总长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
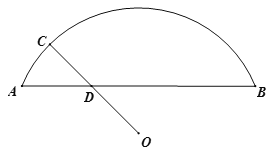
【题目】如图,O是![]() 所在圆的圆心,C是
所在圆的圆心,C是![]() 上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为
上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为![]() cm,O,D两点间的距离为
cm,O,D两点间的距离为![]() cm,C,D两点间的距离为
cm,C,D两点间的距离为![]() cm.小腾根据学习函数的经验,分别对函数
cm.小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.10 | 8.00 | 9.35 |
| 4.93 | 3.99 |
| 2.28 | 1.70 | 1.59 | 2.04 | 2.88 | 3.67 | 4.93 |
| 0.00 | 0.94 | 1.83 | 2.65 | 3.23 | 3.34 | 2.89 | 2.05 | 1.26 | 0.00 |
(2)①在同一平面直角坐标系![]() 中,描出表中各组数值所对应的点(
中,描出表中各组数值所对应的点(![]() ,
,![]() ), (
), (![]() ,
,![]() ),并画出(1)中所确定的函数
),并画出(1)中所确定的函数![]() ,
,![]() 的图象;
的图象;
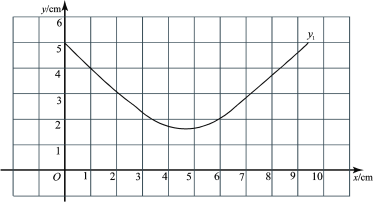
②观察函数![]() 的图象,可得
的图象,可得![]() cm(结果保留一位小数);
cm(结果保留一位小数);
(
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=a与抛物线![]() 交于A、B两点(A在B的左侧),交y轴于点C
交于A、B两点(A在B的左侧),交y轴于点C
(1)若AB=4,求a的值
(2)若抛物线上存在点D(不与A、B重合),使![]() ,求a的取值范围
,求a的取值范围
(3)如图2,直线y=kx+2与抛物线交于点E、F,点P是抛物线上的动点,延长PE、PF分别交直线y=-2于M、N两点,MN交y轴于Q点,求QM·QN的值。
图1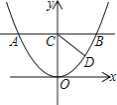 图2
图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com