
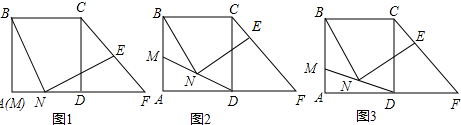
分析 (1)作EG∥CD于G,证明DN=DG=EF=EG,即可得出tan∠ENF的值;
(2)延长BN交CD的延长线于G,作EH⊥CE交CD于H;先证明GN=BN,再证明NE=BN=GN=$\frac{1}{2}$BG,得出∠BEG=90°,然后证明BCE≌△GHE,得出BE=GE,即可得出结论;
(3)设CE=a,则EF=2a,CF=3a,根据题意求出AD、AM即可得出结果.
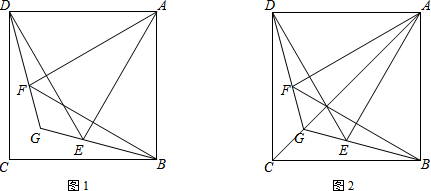
解答 (1)解:作EG∥CD于G,如图1所示: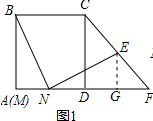 ∵E为CF的中点,
∵E为CF的中点,
∴DG=FG=$\frac{1}{2}$DF,EG=$\frac{1}{2}$CD,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∵DF=DC,
∴AD=DF,
∵N为MD的中点,
∴DN=$\frac{1}{2}$AD,
∴DN=DG=EF=EG,
∴tan∠ENF=$\frac{EG}{NG}$=$\frac{1}{2}$;
(2)证明:延长BN交CD的延长线于G,作EH⊥CE交CD于H;如图2所示: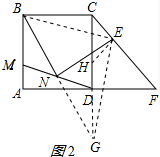
∵N为MD的中点,
∴DN=MN,
∵AB∥CG,
∴$\frac{GN}{BN}=\frac{DN}{MN}$=1,
∴GN=BN,
∵BN=NE,
∴NE=BN=GN=$\frac{1}{2}$BG,
∴∠BEG=90°,
∵EH⊥CE,
∴∠CEH=90°,
∴∠BEC=∠GEH,
∵∠CDF=180°-90°=90°,DF=DC,
∴∠DCF=45°,
∴∠CHE=45°,∠BCE=135°,
∴CE=HE,∠GHE=135°,
∴∠BCE=∠GHE,
在△BCE和△GHE中,
$\left\{\begin{array}{l}{∠BEC=∠GEH}&{\;}\\{CE=HE}&{\;}\\{∠BCE=∠GHE}&{\;}\end{array}\right.$,
∴△BCE≌△GHE(ASA),
∴BE=GE,
∴BN⊥NE;
(3)解:设CE=a,则EF=2a,CF=3a,
∴CD=BC=AB=AD=$\frac{3\sqrt{2}}{2}$a,CH=$\sqrt{2}$a,
∴DH=$\frac{\sqrt{2}}{2}$a,
∵△BCE≌△GHE,
∴GH=BC=$\frac{3\sqrt{2}}{2}$a,
∴DG=$\sqrt{2}$a,
∴BM=$\sqrt{2}$a,
∴AM=$\frac{\sqrt{2}}{2}$a,
∴tan∠ADM=$\frac{AM}{AD}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{3\sqrt{2}}{2}}$=$\frac{1}{3}$.
点评 本题是四边形综合题,考查了正方形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,等腰直角三角形的判定与性质,锐角三角函数等知识;难度较大,综合性强,通过作辅助线构造出全等三角形与等腰直角三角形是解题的关键,也是解题的难点.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高查看答案和解析>>
科目:初中数学 来源: 题型:填空题
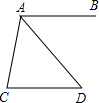 如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D等于多少度?
如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D等于多少度?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com