
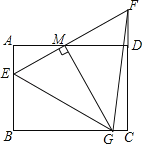
【题目】如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC于G.
(1)若M为边AD中点,求证:△EFG是等腰三角形;
(2)若点G与点C重合,求线段MG的长;
(3)请用含a的代数式表示△EFG的面积S,并指出S的最小整数值.
【答案】(1)见解析;(2)![]() ;(3)S=
;(3)S=![]() +6,S的最小整数值为7
+6,S的最小整数值为7
【解析】
(1)利用△MAE≌△MDF,求出EM=FM,再由MG⊥EM,得出EG=FG,所以△EFG是等腰三角形;
(2)利用勾股定理EM2=AE2+AM2,EC2=BE2+BC2,得出CM2=EC2-EM2,利用线段关系求出CM.再△MAE∽△CDM,求出a的值,再求出CM.
(3)①当点M在AD上时,②:①当点M在AD的延长线上时,作MN⊥BC,交BC于点N,先求出EM,再利用△MAE∽△MDF求出FM,得到EF的值,再由△MNG∽△MAE得出MG的长度,然后用含a的代数式表示△EFG的面积S,指出S的最小整数值.
(1)∵四边形ABCD是矩形,
∴∠A=∠MDF=90°,
∵M为边AD中点,
∴MA=MD
在△MAE和△MDF中,
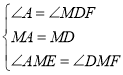
∴△MAE≌△MDF(ASA),
∴EM=FM,
又∵MG⊥EM,
∴EG=FG,
∴△EFG是等腰三角形;
(2)解:如图1,
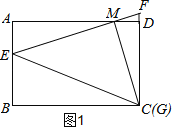
∵AB=3,AD=4,AE=1,AM=a
∴BE=AB﹣AE=3﹣1=2,BC=AD=4,
∴EM2=AE2+AM2,EC2=BE2+BC2,
∴EM2=1+a2,EC2=4+16=20,
∵CM2=EC2﹣EM2,
∴CM2=20﹣1﹣a2=19﹣a2,
∴CM=![]() .
.
∵AB∥CD,
∴∠AEM=∠MFD,
又∵∠MCD+∠MFD=90°,∠AME+∠AEM=90°,
∴∠AME=∠MCD,
∵∠MAE=∠CDM=90°,
∴△MAE∽△CDM,
∴![]() ,即
,即![]() ,
,
解得a=1或3,
代入CM=![]() ,
,
得![]() .
.
(3)解::①当点M在AD上时,如图2,作MN⊥BC,交BC于点N,

∵AB=3,AD=4,AE=1,AM=a
∴![]() ,MD=AD﹣AM=4﹣a,
,MD=AD﹣AM=4﹣a,
∵∠A=∠MDF=90°,∠AME=∠DMF,
∴△MAE∽△MDF
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AD∥BC,
∴∠MGN=∠DMG,
∵∠AME+∠AEM=90°,∠AME+∠DMG=90°,
∴∠AME=∠DMG,
∴∠MGN=∠AME,
∵∠MNG=∠MAE=90°,
∴△MNG∽△MAE
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即S=![]() +6,
+6,
当a=![]() ,S有最小整数值,S=1+6=7.
,S有最小整数值,S=1+6=7.
②当点M在AD的延长线上时,如图3,作MN⊥BC,交BC延长线于点N,
∵AB=3,AD=4,AE=1,AM=a,
∴![]() ,MD=a-4,
,MD=a-4,
∵DC∥AB,
∴△MAE∽△MDF
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠AME+∠EMN=90°,∠NMG+∠EMN=90°,
∴∠AME=∠NMG,
∵∠MNG=∠MAE=90°,
∴△MNG∽△MAE
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
即S=![]() +6,
+6,
当a>4时,S没有整数值.
综上所述当a=![]() 时,S有最小整数值,S=1+6=7.
时,S有最小整数值,S=1+6=7.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家医保局相关负责人3月25日表示,2019年底前我国将实现生育保险基金并入职工基本医疗保险基金,统一征缴,就是通常所说的“五险变四险”.传统的五险包括:养老保险、失业保险、医疗保险、工伤保险、生育保险.某单位从这五险中随机抽取两种,为员工提高保险比例,则正好抽中养老保险和医疗保险的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
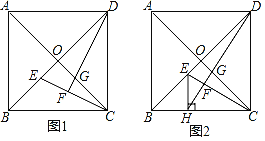
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
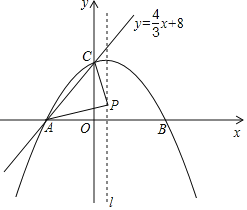
【题目】如图,在平面直角坐标系中,直线AC:y=![]() x+8与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A,C,且与x轴的另一交点为B,又点P是抛物线的对称轴l上一动点.若△PAC周长的最小值为10+2
x+8与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A,C,且与x轴的另一交点为B,又点P是抛物线的对称轴l上一动点.若△PAC周长的最小值为10+2![]() ,则抛物线的解析式为_____.
,则抛物线的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接疫情彻底结束后的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且甲种运动鞋的数量不超过100双,问该专卖店共有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图形![]() 和图形
和图形![]() 上的两点
上的两点![]() 、
、![]() ,如果
,如果![]() 上的所有点都在图形
上的所有点都在图形![]() 的内部或边上,则称
的内部或边上,则称![]() 为图形
为图形![]() 的内弧.特别的,在
的内弧.特别的,在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在
上的所有点都在![]() 的内部或边上,则称
的内部或边上,则称![]() 为
为![]() 的中内弧.(注:
的中内弧.(注:![]() 是指劣弧或半圆)在平面直角坐标系中,已知点
是指劣弧或半圆)在平面直角坐标系中,已知点![]()
![]() .设内弧所在圆的圆心为
.设内弧所在圆的圆心为![]() .
.
(1)当![]() 时,连接
时,连接![]() 、
、![]() 并延长.
并延长.
①请在图1中画出一条![]() 的内弧
的内弧![]() ;
;
②请直接写出![]() 的内弧
的内弧![]() 长度的最大值__________.
长度的最大值__________.
(2)连接![]() 、
、![]() 并延长.
并延长.
①当![]() 时,请直接写出
时,请直接写出![]() 的所有内弧
的所有内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标的取值范围__________;
的纵坐标的取值范围__________;
②若直线![]() 上存在
上存在![]() 的内弧
的内弧![]() 所在圆的圆心
所在圆的圆心![]() ,请求出
,请求出![]() 的取值范围.
的取值范围.
(3)作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .令
.令![]() ,当
,当![]() 的中内弧
的中内弧![]() 所在的圆的圆心
所在的圆的圆心![]() 在
在![]() 的外部时,
的外部时,![]() 的所有中内弧
的所有中内弧![]() 都存在,请直接写出
都存在,请直接写出![]() 的取值范围__________.
的取值范围__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程:

已知:如图,直线![]() 和直线
和直线![]() 外一点
外一点![]() 求作:直线
求作:直线![]() ,使得
,使得![]()
作法:如图
①在直线![]() 上任取一点
上任取一点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径画圆,与直线
为半径画圆,与直线![]() 交于点
交于点![]() ,
,![]() 两点
两点
②连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]()
③作![]() 的平分线
的平分线![]() ,并反向延长
,并反向延长
所以直线![]() 就是所求做的直线
就是所求做的直线
根据小星同学设计的尺规作图过程,
(1)使用直尺和圆规,保全图形(保留作图痕迹)
(2)完成下面的证明
证明:![]() ,
,
![]() (_______________________)(填推理的依据)
(_______________________)(填推理的依据)
![]() 是
是![]() 的外角
的外角
![]() .
.
![]() 平分
平分![]() __________________
__________________
![]() (____________________)(填推理的依据)
(____________________)(填推理的依据)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com