
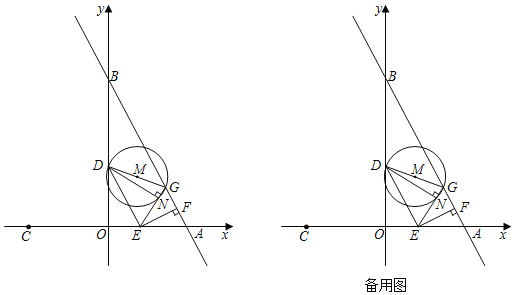
°æƒø°ø»ÁÕº£¨÷±œþy£Ω©Å2x+6”Îx÷·£¨y÷·∑÷±ΩªA£¨B¡Ωµ„£¨µ„Aπÿ”⁄‘≠µ„Oµƒ∂‘≥∆µ„ «µ„C£¨∂ص„E¥”A≥ˆ∑¢“‘√ø√Î1∏ˆµ•ŒªµƒÀŸ∂»‘À∂ØµΩµ„C£¨µ„D‘⁄œþ∂ŒOB…œ¬˙◊„tan°œDEO£Ω2£¨π˝Eµ„◊˜EF°ÕAB”⁄µ„F£¨µ„Aπÿ”⁄µ„Fµƒ∂‘≥∆µ„Œ™µ„G£¨“‘DGŒ™÷±æ∂◊˜°—M£¨…˵„E‘À∂صƒ ±º‰Œ™t√Σª
£®1£©µ±µ„E‘⁄œþ∂ŒOA…œ‘À∂Ø£¨t£Ω°°°° ±£¨°˜AEF”ΰ˜EDOµƒœýÀ∆±»Œ™1£∫![]() £ª
£ª
£®2£©µ±°—M”Îy÷·œý«– ±£¨«Ûtµƒ÷µ£ª
£®3£©»Ù÷±œþEG”ΰ—MΩª”⁄µ„N£¨ «∑ҥʑ⁄t πNG£Ω![]() £¨»Ù¥Ê‘⁄£¨«Û≥ˆtµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
£¨»Ù¥Ê‘⁄£¨«Û≥ˆtµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©t£Ω
£ª£®2£©t£Ω![]() ªÚ5£ª£®3£©¥Ê‘⁄£¨t£Ω
ªÚ5£ª£®3£©¥Ê‘⁄£¨t£Ω![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() £Æ
£Æ
°æΩ‚Œˆ°ø
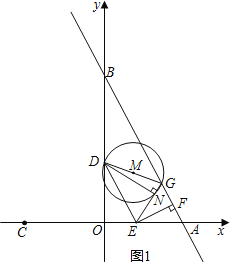
£®1£©œ»«Û÷±œþ”Î◊¯±Í÷·µƒΩªµ„◊¯±Í£¨‘Ÿ÷§°˜AEF°◊°˜EDO°◊°˜ABO£¨”…°˜AEF”ΰ˜EDOµƒœýÀ∆±»Œ™1£∫![]() £¨º¥ø…«Ûµ√tµƒ÷µ£ª
£¨º¥ø…«Ûµ√tµƒ÷µ£ª
£®2£©”…°—M”Îy÷·œý«–ø…÷™£∫DG°Õy÷·£¨∑÷¡Ω÷÷«Èøˆ£∫0°Ðt°Ð3ªÚ3£ºt°Ð6£¨∑÷±”…D°¢Gµƒ◊ð◊¯±Íœýµ»Ω®¡¢∑Ω≥ëÛΩ‚º¥ø…£ª
£®3£©∑÷»˝÷÷«Èøˆ£∫0°Ðt°Ð![]() ªÚ
ªÚ![]() £ºt°Ð3ªÚ3£ºt°Ð6£¨∑÷±Ω®¡¢∑Ω≥ëÛΩ‚º¥ø…£Æ
£ºt°Ð3ªÚ3£ºt°Ð6£¨∑÷±Ω®¡¢∑Ω≥ëÛΩ‚º¥ø…£Æ
Ω‚£∫£®1£©‘⁄y£Ω©Å2x+6÷–£¨¡Óx£Ω0£¨µ√£∫y£Ω6£¨
¡Óy£Ω0£¨µ√£∫©Å2x+6£Ω0£¨
Ω‚µ√£∫x£Ω3£¨
°ýA£®3£¨0£©£¨B£®0£¨6£©£¨C£®©Å3£¨0£©
°ýOA£Ω3£¨OB£Ω6£¨AB£Ω3![]() £¨AE£Ωt£¨OE£Ω3©Åt£¨
£¨AE£Ωt£¨OE£Ω3©Åt£¨
°ýtan°œBAO£Ω![]() £Ω2
£Ω2
°þtan°œDEO£Ω2
°ý°œBAO£Ω°œDEO
°þEF°ÕAB
°ý°œAFE£Ω°œDOE£Ω90°„
°ý°˜AEF°◊°˜EDO°◊°˜ABO
![]() £¨º¥
£¨º¥![]()
°ýAF£Ω![]() t£ª
t£ª
°þ°˜AEF”ΰ˜EDOµƒœýÀ∆±»Œ™1£∫![]() £¨
£¨
°ý![]() £¨º¥OE£Ω
£¨º¥OE£Ω![]() AF
AF
°ý3©Åt£Ω![]() °¡
°¡![]() t£¨
t£¨
Ω‚µ√£∫t£Ω![]() £ª
£ª
π ¥∞∏Œ™£∫t£Ω![]() £ª
£ª
£®2£©°þ°—M”Îy÷·œý«–
°ýDG°Õy÷·
µ±0°Ðt°Ð3 ±£¨![]()
°þtan°œDEO£Ω2
°ý![]()
°ý![]()
°þ![]() £¨°˜AEF°◊°˜ABO
£¨°˜AEF°◊°˜ABO
°ý![]()
°ý![]()
°þµ„A°¢Gπÿ”⁄µ„F∂‘≥∆
°ý![]()
°ý![]()
Ω´![]() ¥˙»Î
¥˙»Î![]() ÷–£¨µ√£¨
÷–£¨µ√£¨![]()
Ω‚µ√![]() £¨
£¨
°ýG£®3©Å![]() t£¨
t£¨![]() t£©£¨D£®0£¨6©Å2t£©£¨
t£©£¨D£®0£¨6©Å2t£©£¨
°ý![]() t£Ω6©Å2t£¨Ω‚µ√£∫t£Ω
t£Ω6©Å2t£¨Ω‚µ√£∫t£Ω![]() £ª
£ª
µ±3£ºt°Ð6 ±£¨Õ¨¿Ìµ√G£®3©Å![]() t£¨
t£¨![]() t£©£¨D£®0£¨2t©Å6£©£¨
t£©£¨D£®0£¨2t©Å6£©£¨
°ý![]() t£Ω2t©Å6£¨Ω‚µ√£∫t£Ω5£¨
t£Ω2t©Å6£¨Ω‚µ√£∫t£Ω5£¨
◊€…œÀ˘ ˆ£¨µ±°—M”Îy÷·œý«– ±£¨t£Ω![]() ªÚ5£ª
ªÚ5£ª
£®3£©¥Ê‘⁄£Æ
µ±0°Ðt°Ð![]() ±£¨G£®3©Å
±£¨G£®3©Å![]() t£¨
t£¨![]() t£©£¨D£®0£¨6©Å2t£©£¨
t£©£¨D£®0£¨6©Å2t£©£¨
°þµ„Aπÿ”⁄µ„Fµƒ∂‘≥∆µ„Œ™µ„G£¨EF°ÕAB
°ýEG£ΩEA£Ωt
°þ°œOEG£Ω°œOAB+°œEGA£Ω2°œOAB£¨°œOED£Ω°œOAB
°ý°œGED£Ω°œOED£Ω°œOAB
°þDGŒ™÷±æ∂
°ý°œDNG£Ω°œDNE£Ω°œDOE£Ω90°„£¨DE£ΩDE
°ý°˜DEN°’°˜DEO£®AAS£©
°ýEN£ΩOE£Ω3©Åt£¨NG£ΩEN©ÅEG£Ω3©Åt©Åt£Ω3©Å2t£¨
°ý3©Å2t£Ω![]() £¨
£¨
Ω‚µ√£∫t£Ω![]() £¨
£¨
µ±![]() £ºt°Ð3 ±£¨NG£ΩEG©ÅEN£Ωt©Å£®3©Åt£©£Ω2t©Å3
£ºt°Ð3 ±£¨NG£ΩEG©ÅEN£Ωt©Å£®3©Åt£©£Ω2t©Å3
°ý2t©Å3£Ω![]() £¨
£¨
Ω‚µ√£∫t£Ω![]() £ª
£ª
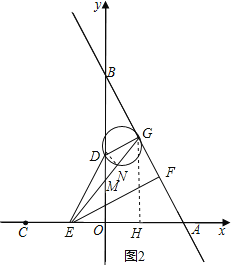
µ±3£ºt°Ð6 ±£¨»ÁÕº2£¨¡¨Ω”DN£¨π˝G◊˜GH°Õx÷·”⁄H£¨
°þDG «÷±æ∂£¨
°ý°œDNG£Ω°œDNE£Ω90°„£¨
°þ°œDMN£Ω°œEMO
°ý°˜DMN°◊°˜EMO
°ý°œMDN£Ω°œOEM
°þGH°Œy÷·
°ý![]() £¨º¥
£¨º¥![]() £¨
£¨
”…£®2£©µ√![]() £¨
£¨
°þ![]() ÷·£¨
÷·£¨
°ý![]() £¨
£¨![]() £¨
£¨
°ý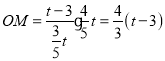 £¨
£¨
°ýDM£ΩOD©ÅOM£Ω2£®t©Å3£©©Å![]() £®t©Å3£©£Ω
£®t©Å3£©£Ω![]() £®t©Å3£©
£®t©Å3£©
°þtan°œOEM£Ω![]()
°ýEM£Ω![]() OE£Ω
OE£Ω![]() £®t©Å3£©£¨
£®t©Å3£©£¨
°ýsin°œOEM£Ω![]() £Ω
£Ω![]() £Ωsin°œMDN£Ω
£Ωsin°œMDN£Ω![]()
°ýMN£Ω![]() °¡
°¡![]() £®t©Å3£©£Ω
£®t©Å3£©£Ω![]() £®t©Å3£©
£®t©Å3£©
°ýNG£ΩEG©ÅEM©ÅMN£Ωt©Å![]() £®t©Å3£©©Å
£®t©Å3£©©Å![]() £®t©Å3£©£Ω
£®t©Å3£©£Ω![]() ©Å
©Å![]() t£¨
t£¨
°ý![]() £¨
£¨
Ω‚µ√£∫t£Ω![]() £ª
£ª
◊€…œÀ˘ ˆ£¨t£Ω![]() ªÚ
ªÚ![]() ªÚ
ªÚ![]() £Æ
£Æ


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™≈◊ŒÔœþ![]() ”Î∑¥±»¿˝∫Ø ˝
”Î∑¥±»¿˝∫Ø ˝![]() µƒÕºœÒ‘⁄µ⁄“ªœÛœÞ”–“ª∏ˆπ´π≤µ„£¨∆‰∫·◊¯±ÍŒ™1£¨‘Ú“ª¥Œ∫Ø ˝
µƒÕºœÒ‘⁄µ⁄“ªœÛœÞ”–“ª∏ˆπ´π≤µ„£¨∆‰∫·◊¯±ÍŒ™1£¨‘Ú“ª¥Œ∫Ø ˝![]() µƒÕºœÒø…ƒÐ «£® £©
µƒÕºœÒø…ƒÐ «£® £©
A. 
B. 
C. 
D. 
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–°√˜º“À˘‘⁄æ”√Ò¬•µƒ∂‘√Ê”–“ª◊˘¥Ûœ√AB£¨∏þŒ™74√◊£¨Œ™≤‚¡øæ”√Ò¬•”Î¥Ûœ√÷ƺ‰µƒæý¿Î£¨–°√˜¥”◊‘º∫º“µƒ¥∞ªßC¥¶≤‚µ√¥Ûœ√∂•≤øAµƒ—ˆΩ«Œ™37°„£¨¥Ûœ√µ◊≤øBµƒ∏©Ω«Œ™48°„£Æ
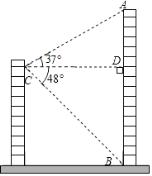
£®1£©«Û°œACBµƒ∂» ˝£ª
£®2£©«Û–°√˜º“À˘‘⁄æ”√Ò¬•”Î¥Ûœ√÷ƺ‰µƒæý¿Î£Æ£®≤Œøº ˝æð£∫sin37°„°÷![]() £¨cos37°„°÷
£¨cos37°„°÷![]() £¨tan37°„°÷
£¨tan37°„°÷![]() £¨sin48°„°÷
£¨sin48°„°÷![]() £¨cos48°„°÷
£¨cos48°„°÷![]() £¨tan48°„°÷
£¨tan48°„°÷![]() £©
£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ»—¸Rt°˜ABCµƒ÷±Ω«±þ≥§Œ™4£¨“‘AŒ™‘≤–ƒ£¨÷±Ω«±þABŒ™∞Îæ∂◊˜ª°BC1£¨Ωª–±±þAC”⁄µ„C1£¨C1B1°ÕAB”⁄µ„B1£¨…˪°BC1£¨C1B1£¨B1BŒß≥…µƒ“ı”∞≤ø∑÷µƒ√ʪ˝Œ™S1£¨»ª∫Û“‘AŒ™‘≤–ƒ£¨AB1Œ™∞Îæ∂◊˜ª°B1C2£¨Ωª–±±þAC”⁄µ„C2£¨C2B2°ÕAB”⁄µ„B2£¨…˪°B1C2£¨C2B2£¨B2B1Œß≥…µƒ“ı”∞≤ø∑÷µƒ√ʪ˝Œ™S2£¨∞¥¥Àπʬ…ºÃ–¯◊˜œ¬»•£¨µ√µΩµƒ“ı”∞≤ø∑÷µƒ√ʪ˝S3£Ω_____£Æ
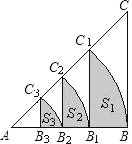
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨÷±œþy£Ω![]() x+6”Î∑¥±»¿˝∫Ø ˝y£Ω
x+6”Î∑¥±»¿˝∫Ø ˝y£Ω![]() £®k£æ0£©µƒÕºœÛΩª”⁄µ„M°¢N£¨”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„B°¢A£¨◊˜ME°Õx÷·”⁄µ„E£¨NF°Õx÷·”⁄µ„F£¨π˝µ„E°¢F∑÷±◊˜EG°ŒAB£¨FH°ŒAB£¨∑÷±Ωªy÷·”⁄µ„G°¢H£¨MEΩªHF”⁄µ„K£¨»ÙÀƒ±þ–ŒMKFN∫ÕÀƒ±þ–ŒHGEKµƒ√ʪ˝∫ÕŒ™12£¨‘Úkµƒ÷µŒ™_____£Æ
£®k£æ0£©µƒÕºœÛΩª”⁄µ„M°¢N£¨”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„B°¢A£¨◊˜ME°Õx÷·”⁄µ„E£¨NF°Õx÷·”⁄µ„F£¨π˝µ„E°¢F∑÷±◊˜EG°ŒAB£¨FH°ŒAB£¨∑÷±Ωªy÷·”⁄µ„G°¢H£¨MEΩªHF”⁄µ„K£¨»ÙÀƒ±þ–ŒMKFN∫ÕÀƒ±þ–ŒHGEKµƒ√ʪ˝∫ÕŒ™12£¨‘Úkµƒ÷µŒ™_____£Æ
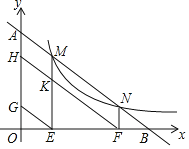
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ «“ª’≈∂ÐππÀ̵¿∂œ√ÊΩ·ππÕº£ÆÀ̵¿ƒ⁄≤øŒ™“‘OŒ™‘≤–ƒ£¨ABŒ™÷±æ∂µƒ‘≤£ÆÀ̵¿ƒ⁄≤øπ≤∑÷Œ™»˝≤„£¨…œ≤„Œ™≈≈—õ¿£¨÷–º‰Œ™––≥µÀ̵¿£¨œ¬≤„Œ™∑˛ŒÒ≤„£Æµ„AµΩ∂•≈Ôµƒæý¿ÎŒ™1.6m£¨∂•≈ÔµΩ¬∑√ʵƒæý¿Î «6.4m£¨µ„BµΩ¬∑√ʵƒæý¿ÎŒ™4.0m£Æ«Î«Û≥ˆ¬∑√ÊCDµƒøÌ∂»£Æ£®æ´»∑µΩ0.1m£©
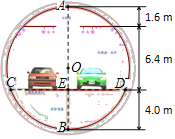
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
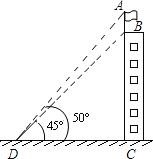
°æƒø°ø≤‚¡øº∆À„ «»’≥£…˙ªÓ÷–≥£º˚µƒŒ £¨»ÁÕº£¨Ω®÷˛ŒÔBCµƒŒð∂•”–“ª∏˘∆Ï∏ÀAB£¨¥”µÿ√Ê…œDµ„¥¶π€≤‚∆Ï∏À∂•µ„Aµƒ—ˆΩ«Œ™50°„£¨π€≤‚∆Ï∏Àµ◊≤øBµ„µƒ—ˆΩ«Œ™45°„£¨£®ø…”√µƒ≤Œøº ˝æð£∫sin50°„°÷0.8£¨tan50°„°÷1.2£©
£®1£©»Ù“—÷™CD=20√◊£¨«ÛΩ®÷˛ŒÔBCµƒ∏þ∂»£ª
£®2£©»Ù“—÷™∆Ï∏Àµƒ∏þ∂»AB=5√◊£¨«ÛΩ®÷˛ŒÔBCµƒ∏þ∂»£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ Â÷≥ˆ
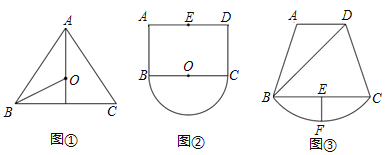
£®1£©»ÁÕº¢Ÿ£¨‘⁄°˜ABC÷–£¨AB£ΩAC£Ω10£¨BC£Ω12£¨µ„O «°˜ABCµƒÕ‚Ω”‘≤µƒ‘≤–ƒ£¨‘ÚOBµƒ≥§Œ™°° °°
Œ ÂÃΩæø
£®2£©»ÁÕº¢⁄£¨“—÷™æÿ–ŒABCD£¨AB£Ω4£¨AD£Ω6£¨µ„EŒ™ADµƒ÷–µ„£¨“‘BCŒ™÷±æ∂◊˜∞Α≤O£¨µ„PŒ™∞Α≤O…œ“ª∂ص„£¨«ÛE°¢P÷ƺ‰µƒ◊Ó¥Ûæý¿Î£ª
Œ Ã‚Ω‚æˆ
£®3£©ƒ≥µÿ”–“ªøÈ»ÁÕº¢€À˘ 浃π˚‘∞£¨π˚‘∞ «”…Àƒ±þ–ŒABCD∫Õœ“CB”Î∆‰À˘∂‘µƒ¡”ª°≥°µÿ◊È≥…µƒ£¨π˚‘∞÷˜»Àœ÷“™¥”»Îø⁄DµΩ![]() …œµƒ“ªµ„P–ÞΩ®“ªÃı± ÷±µƒ–°¬∑DP£Æ“—÷™AD°ŒBC£¨°œADB£Ω45°„£¨BD£Ω120
…œµƒ“ªµ„P–ÞΩ®“ªÃı± ÷±µƒ–°¬∑DP£Æ“—÷™AD°ŒBC£¨°œADB£Ω45°„£¨BD£Ω120![]() √◊£¨BC£Ω160√◊£¨π˝œ“BCµƒ÷–µ„E◊˜EF°ÕBCΩª
√◊£¨BC£Ω160√◊£¨π˝œ“BCµƒ÷–µ„E◊˜EF°ÕBCΩª![]() ”⁄µ„F£¨”÷≤‚µ√EF£Ω40√◊£Æ–ÞΩ®–°¬∑∆Ωæ˘√ø√◊–Ë“™40‘™£®–°¬∑øÌ∂»≤ªº∆£©£¨≤ªøº¬«∆‰À˚“ÚÀÿ£¨«Îƒ„∏˘æð“‘…œ–≈œ¢£¨∞Ô÷˙π˚‘∞÷˜»Àº∆À„–ÞΩ®’‚Ãı–°¬∑◊Ó∂ý“™ª®∑—∂ý…Ÿ‘™£ø
”⁄µ„F£¨”÷≤‚µ√EF£Ω40√◊£Æ–ÞΩ®–°¬∑∆Ωæ˘√ø√◊–Ë“™40‘™£®–°¬∑øÌ∂»≤ªº∆£©£¨≤ªøº¬«∆‰À˚“ÚÀÿ£¨«Îƒ„∏˘æð“‘…œ–≈œ¢£¨∞Ô÷˙π˚‘∞÷˜»Àº∆À„–ÞΩ®’‚Ãı–°¬∑◊Ó∂ý“™ª®∑—∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
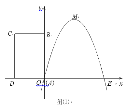
°æƒø°ø»ÁÕº£®1£©£¨“—÷™≈◊ŒÔœþæ≠π˝◊¯±Í‘≠µ„O∫Õx÷·…œ¡Ì“ªµ„E£¨∂•µ„Mµƒ◊¯±ÍŒ™(2£¨4)£ªæÿ–ŒABCDµƒ∂•µ„A”ε„O÷ÿ∫œ£¨AD°¢AB∑÷±‘⁄x÷·°¢y÷·…œ£¨«“AD=2£¨AB=3£Æ
£®1£©«Û÷±œþy=3”Î≈◊ŒÔœþΩªµ„µƒ◊¯±Í£ª
£®2£©Ω´æÿ–ŒABCD“‘√ø√Î1∏ˆµ•Œª≥§∂»µƒÀŸ∂»¥”Õº¢≈À˘ 浃Œª÷√—ÿx÷·µƒ’˝∑ΩœÚ‘»ÀŸ∆Ω––“∆∂Ø£¨Õ¨ ±“ª∂ص„P“≤“‘œýÕ¨µƒÀŸ∂»¥”µ„A≥ˆ∑¢œÚB‘»ÀŸ“∆∂Ø£¨…ËÀ¸√«‘À∂صƒ ±º‰Œ™t√Σ®0°Ðt°Ð3£©£¨÷±œþAB”Î∏√≈◊ŒÔœþµƒΩªµ„Œ™N£®»ÁÕº£®2£©À˘ 棩£Æ
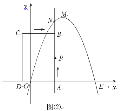
¢Ÿµ±![]() ±£¨≈–∂œµ„P «∑Ò‘⁄÷±œþME…œ£¨≤¢Àµ√˜¿Ì”…£ª
±£¨≈–∂œµ„P «∑Ò‘⁄÷±œþME…œ£¨≤¢Àµ√˜¿Ì”…£ª
¢⁄…Ë“‘P°¢N°¢C°¢DŒ™∂•µ„µƒ∂ý±þ–Œ√ʪ˝Œ™S£¨ ‘Œ S «∑ҥʑ⁄◊Ó¥Û÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ’‚∏ˆ◊Ó¥Û÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com